Diffie-Hellman

Come possono due persone in una stanza affollata derivare un segreto che solo la coppia conoscere, senza rivelare il segreto a chiunque altro, che potrebbe essere in ascolto?

Questo è esattamente lo scenario che lo scambio di chiavi Diffie-Hellman esiste per risolvere.

Lo scambio di chiavi Diffie-Hellman è un mezzo per due parti per stabilire congiuntamente un segreto condiviso su un canale non sicuro, senza avere alcuna conoscenza preliminare l’uno dell’altro.

In realtà non scambiano mai il segreto, solo alcuni valori che entrambi combinano che consentono loro di raggiungere lo stesso valore risultante.

Concettualmente, il modo migliore per visualizzare lo scambio di chiavi Diffie-Hellman è con l’onnipresente dimostrazione di miscelazione del colore della vernice. Vale la pena rivederlo rapidamente se non si ha familiarità con esso.

Tuttavia, in questo articolo vogliamo fare un ulteriore passo avanti e mostrarti effettivamente la matematica nello scambio di chiavi Diffie-Hellman.

DH Math

Prima di entrare nella matematica di Diffie-Hellman, vorrai avere una comprensione di base di cosa sia un numero Primo e quale sia l’operazione del Modulo (aka, divisione del resto). Entrambi questi termini sono stati definiti in un altro articolo.

Di seguito è riportata un’infografica che illustra tutti i passaggi dello scambio Diffie-Hellman tra Alice e Bob.

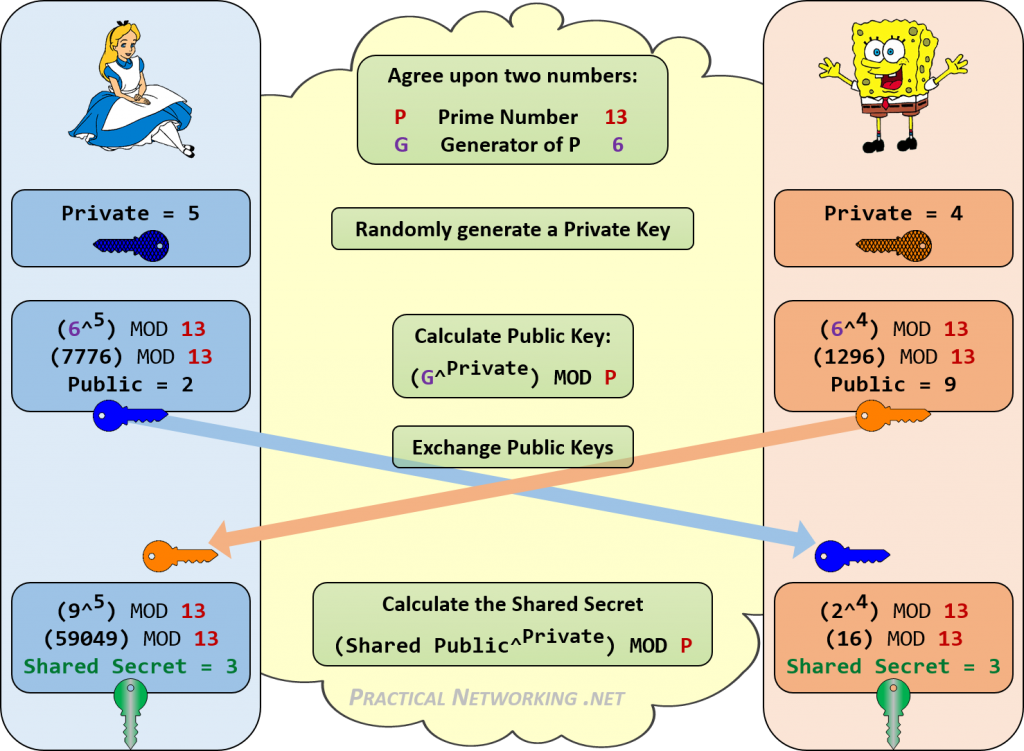
Si noti come sia Alice che Bob sono stati in grado di raggiungere lo stesso Segreto condiviso di 3. Chiunque ascolti il proprio scambio di chiavi DH conoscerebbe solo i valori pubblici e i valori P e G iniziali. Non esiste un modo coerente per combinare quei numeri (13, 6, 2, 9) per raggiungere 3.

Numeri DH

Nel nostro esempio, abbiamo usato un numero Primo di 13. Poiché questo numero Primo viene utilizzato anche come Modulo per ogni calcolo, l’intero spazio chiave per il Segreto condiviso risultante può essere sempre 0-12. Più grande è questo numero, più difficile sarà un momento in cui un utente malintenzionato forzerà il tuo segreto condiviso.

Ovviamente, stavamo usando numeri molto piccoli sopra per aiutare a mantenere la matematica relativamente semplice. I veri scambi DH stanno facendo matematica su numeri che sono molto più grandi. Ci sono tre dimensioni tipiche per i numeri in Diffie-Hellman:

La dimensione del bit è un riferimento al numero Primo. Ciò equivale direttamente all’intero spazio chiave del Segreto condiviso risultante. Per darti un’idea di quanto sia grande questo spazio chiave:

Per scrivere completamente un numero a 768 bit, avresti bisogno di 232 cifre decimali.
Per scrivere completamente un numero a 1024 bit, sono necessarie 309 cifre decimali.
Per scrivere completamente un numero a 1536 bit, sono necessarie 463 cifre decimali.

Utilizzo del segreto condiviso

Una volta raggiunto il segreto condiviso, viene in genere utilizzato nel calcolo per stabilire una chiave di crittografia simmetrica congiunta e/o una chiave HMAC congiunta, nota anche come Chiavi di sessione.

Ma è importante sottolineare che il Segreto condiviso stesso non dovrebbe essere usato direttamente come Chiave segreta. Se lo fosse, tutto ciò di cui puoi essere certo è che durante la conversazione sicura stai ancora parlando con la stessa parte che era dall’altra parte dello scambio Diffie-Hellman.

Tuttavia, non hai ancora alcuna conferma o garanzia su chi sia l’altra parte. Solo che nessun altro può tutto ad un tratto fingere di essere loro nel bel mezzo della vostra conversazione sicura.

La generazione delle chiavi di sessione effettive dovrebbe includere il segreto condiviso DH, insieme a qualche altro valore che sarebbe noto solo all’altra parte prevista, come qualcosa dallo schema di autenticazione scelto.

Preferisci i contenuti video al testo? La maggior parte di questo articolo è stato registrato e può essere visualizzato su Youtube:

Esempio di navigazione in serie RSA > >