Diffie-Hellman

¿Cómo pueden dos personas en una habitación llena de gente derivar un secreto que solo la pareja conoce, sin revelar el secreto a nadie más que pueda estar escuchando?

Ese es exactamente el escenario para el que existe el intercambio de claves Diffie-Hellman.

El Intercambio de Claves Diffie-Hellman es un medio para que dos partes establezcan conjuntamente un secreto compartido a través de un canal inseguro, sin tener ningún conocimiento previo el uno del otro.

En realidad, nunca intercambian el secreto, solo algunos valores que se combinan y que les permiten alcanzar el mismo valor resultante.

Conceptualmente, la mejor manera de visualizar el Intercambio de Claves Diffie-Hellman es con la demostración ubicua de mezcla de colores de pintura. Vale la pena revisarlo rápidamente si no está familiarizado con él.

Sin embargo, en este artículo queremos ir un paso más allá y mostrarle las matemáticas en el Intercambio de claves Diffie-Hellman.

DH Math

Antes de entrar en las matemáticas de Diffie-Hellman, querrá tener una comprensión básica de lo que es un número primo y cuál es la operación de módulo (también conocida como división de remanentes). Ambos términos se han definido en otro artículo.

A continuación se muestra una infografía que describe todos los pasos del intercambio Diffie-Hellman entre Alice y Bob.

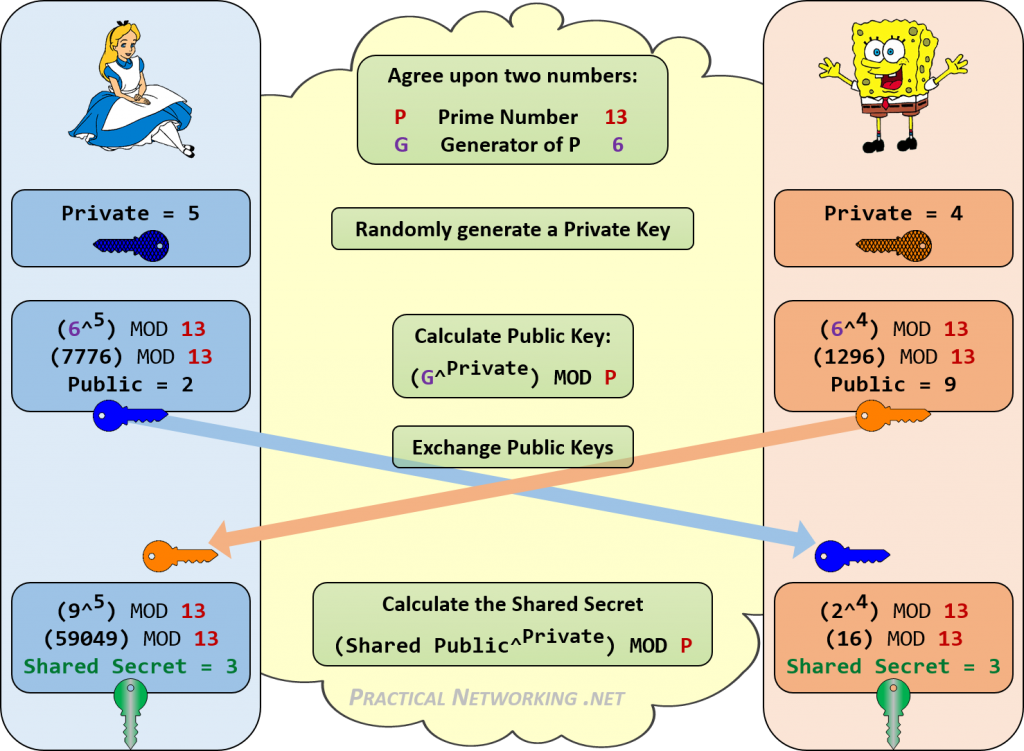
Observe cómo Alice y Bob fueron capaces de alcanzar el mismo Secreto Compartido de 3. Cualquiera que escuche su intercambio de claves DH solo conocerá los Valores Públicos y los valores iniciales de P y G. No hay una manera consistente de combinar esos números (13, 6, 2, 9) para lograr 3.

Números DH

En nuestro ejemplo, usamos un número primo de 13. Dado que este número primo también se usa como Módulo para cada cálculo, el espacio de clave completo para el Secreto Compartido resultante solo puede ser 0-12. Cuanto mayor sea este número,más difícil será el tiempo que tendrá un atacante para forzar su secreto compartido.

Obviamente, estábamos usando números muy pequeños arriba para ayudar a mantener las matemáticas relativamente simples. Los verdaderos intercambios de DH están haciendo matemáticas en números que son mucho más grandes. Hay tres tamaños típicos para los números en Diffie-Hellman:

El tamaño de bits es una referencia al número primo. Esto equivale directamente a todo el espacio de claves del Secreto Compartido resultante. Para darle una idea de cuán grande es este espacio de teclas:

Para escribir completamente un número de 768 bits, necesitaría 232 dígitos decimales.
Para escribir completamente un número de 1024 bits, necesitaría 309 dígitos decimales.
Para escribir completamente un número de 1536 bits, necesitaría 463 dígitos decimales.

Usando el Secreto compartido

Una vez que se ha alcanzado el Secreto Compartido, normalmente se usa en el cálculo para establecer una clave de Cifrado Simétrica conjunta y/o una Clave HMAC conjunta, también conocida como Claves de sesión.

Pero es importante señalar que el Secreto Compartido en sí no debe usarse directamente como Clave Secreta. Si lo fuera, todo lo que puede estar seguro es que a lo largo de la conversación segura sigue hablando con la misma parte que estaba al otro lado del intercambio Diffie-Hellman.

Sin embargo, todavía no tiene confirmación ni garantía de quién es la otra parte. Solo que nadie más puede de repente fingir ser ellos en medio de tu conversación segura.

La generación de las Claves de sesión reales debe incluir el Secreto compartido DH, junto con algún otro valor que solo conozca la otra parte, como algo del esquema de autenticación que eligió.

¿Prefiere el contenido de vídeo al texto? La mayoría de este artículo ha sido grabado y se puede ver en Youtube:

Ejemplo de RSA de navegación de serie > >