Analyse lexicale dans la conception du compilateur

Dans cet article, nous discutons de la première phase de la conception du compilateur où le programme d’entrée de haut niveau est converti en une séquence de jetons. Cette phase est connue sous le nom d’Analyse lexicale dans la conception du compilateur.

Table des matières:

1. Définitions pour l’Analyse Lexicale
2. Un exemple d’Analyse Lexicale
3. Architecture de l’analyseur lexical
4. Expressions régulières
5. Automates finis
6. Relation entre les expressions régulières et les automates finis
7. Règle de correspondance la plus longue
8. Erreurs lexicales
9. Schémas de récupération d’erreurs
10. Besoin d’analyseurs lexicaux
11. Besoin d’analyseurs lexicaux

L’analyse lexicale est le processus de conversion d’une séquence de caractères à partir d’un programme source qui est prise en entrée dans une séquence de jetons.

Une lex est un programme qui génère des analyseurs lexicaux.

Un analyseur lexical / lexer / scanner est un programme qui effectue une analyse lexicale.

Les rôles de l’analyseur lexical impliquent;

• Lecture des caractères d’entrée du programme source.
• Corrélation des messages d’erreur avec le programme source.
• Entrelacement des espaces blancs et des commentaires du programme source.
• Macros d’extension si elles sont trouvées dans le programme source.
• Entrée de jetons identifiés dans la table de symboles.

Le lexème est une instance d’un jeton, c’est-à-dire une séquence de caractères inclus dans le programme source selon le modèle de correspondance d’un jeton.

Un exemple, Étant donné l’expression;
c = a+ b * 5

Les lexèmes et les jetons sont;

Lexèmes	Jetons
identifiant c
=	symbole d’affectation
identifiant a
+	+( symbole d’addition)
identifiant b
*	*( symbole de multiplication)
5	5( nombre)

La séquence de jetons produite par l’analyseur lexical permet à l’analyseur d’analyser la syntaxe d’un langage de programmation.

Un jeton est une séquence valide de caractères donnée par un lexème, il est traité comme une unité dans la grammaire du langage de programmation.
Dans un langage de programmation, cela peut inclure;

• Mots-clés
• Opérateurs
• Symboles de ponctuation
• Constantes
• Identifiants
• Nombres

Un motif est une règle appariée par une séquence de caractères (lexèmes) utilisée par le jeton. Il peut être défini par des expressions régulières ou des règles de grammaire.

Un exemple d’Analyse lexicale

Code

#include<iostream>// exampleint main(){ int a, b; a = 7; return 0;}

Jetons

identifiant

Lexèmes	Jetons
mot-clé int
mot-clé principal
(	opérateur
)	opérateur
{	opérateur
mot-clé int
identifiant a
,	opérateur
d
;	opérateur
identifiant a
=	symbole d’affectation
10	10( nombre)
;	opérateur
retour	mot clé
0	0( nombre)
;	opérateur
}	opérateur

Non Jetons

Type	Jetons
directive du préprocesseur	#include<iostream>
commentaire	// exemple

Le processus d’analyse lexicale se compose de deux étapes.

1. Numérisation – Cela implique la lecture des caractères d’entrée et la suppression des espaces blancs et des commentaires.
2. Tokenisation – C’est la production de jetons en sortie.

Architecture de l’analyseur lexical

La tâche principale de l’analyseur lexical est d’analyser l’ensemble du programme source et d’identifier les jetons un par un.Les scanners
sont implémentés pour produire des jetons à la demande de l’analyseur.

Étapes:

1.  » get next token » est envoyé de l’analyseur à l’analyseur lexical.
2. L’analyseur lexical balaye l’entrée jusqu’à ce que le « jeton suivant » soit localisé.
3. Le jeton est renvoyé à l’analyseur.

Expressions régulières

Nous utilisons des expressions régulières pour exprimer des langages finis en définissant des modèles pour un ensemble fini de symboles.

La grammaire définie par des expressions régulières est connue sous le nom de grammaire régulière et la langue définie par une grammaire régulière est connue sous le nom de langage régulier.
Il existe des règles algébriques obéies par des expressions régulières utilisées pour manipuler des expressions régulières sous des formes équivalentes.

Opérations.

L’Union de deux langues A et B s’écrit comme
A U B = {s|s est en A ou s est en B}
Concaténation de deux langues A et B s’écrit comme
AB = {ss|s est en A et s est en B}
La fermeture kleen d’une langue A s’écrit comme
A* = qui est zéro ou plusieurs occurrences de la langue A.

Notations.

Si x et y sont des expressions régulières désignant les langages A(x) et B(y) alors ;
(x) est une expression régulière désignant A(x).
Union(x)/(y) est une expression régulière désignant A(x)B(y).
La concaténation(x)(y) est une expression régulière bosselant A(x)B(y).
Kleen closure(x) * est une expression régulière indiquant (A(x)) *

Priorité et associativité.

* ‘ concaténation.’ et /(pipe) restent associatifs.
Fermeture Kleen* a la priorité la plus élevée.
Concaténation (.) suit en priorité.
(pipe) / a la priorité la plus basse.

Représentant des jetons valides d’un langage dans des expressions régulières.

X est une expression régulière, donc;

• x * représente zéro occurrence ou plus de x.
• x + représente une ou plusieurs occurrence de x, c’est-à-dire {x, xx, xxx}
• x? représente au plus une occurrence de x ie {x}
• représente tous les alphabets minuscules de la langue anglaise.
• représentent tous les alphabets en majuscules de la langue anglaise.
• représentent tous les nombres naturels.

Représentant l’occurrence de symboles utilisant des expressions régulières
Letter= or
Digit= or |0|1|2|3|4|5|6|7|8|9
Sign=

Représentant des jetons de langue à l’aide d’expressions régulières.
Decimal= (signe)?(chiffre) +
Identificateur = (lettre| (lettre / chiffre) *

Automates finis

Il s’agit de la combinaison de cinq tuples (Q, Σ, q0, qf, δ) se concentrant sur les états et les transitions à travers les symboles d’entrée.
Il reconnaît les motifs en prenant la chaîne de symbole en entrée et change son état en conséquence.
Le modèle mathématique des automates finis se compose de;

• Ensemble fini d’états (Q)
• Ensemble fini de symboles d’entrée (Σ)
• Un état de départ (q0)
• Ensemble d’états finaux (qf)
• Fonction de transition (δ)

Les automates finis sont utilisés en analyse lexicale pour produire des jetons sous forme d’identifiants, de mots-clés et de constantes à partir du programme d’entrée.

Les automates finis alimentent la chaîne d’expression régulière et l’état est modifié pour chaque littéral.

Si l’entrée est traitée avec succès, l’automate atteint l’état final et est accepté sinon il est rejeté.

Construction d’Automates finis

Soit L(r) un langage régulier par certains automates finis F(A).

Par conséquent;

• États: Les cercles représenteront les états de FA et leurs noms sont écrits à l’intérieur des cercles.
• État de démarrage : C’est l’état auquel l’automate démarre. Il aura une flèche pointant vers lui.
• États intermédiaires : Ceux-ci ont deux flèches, l’une pointant vers lui et l’autre pointant des états intermédiaires.
• État final: Les automates sont censés être à l’état final lorsque la chaîne d’entrée a été analysée avec succès et représentée par des doubles cercles sinon l’entrée est rejetée. Il peut contenir un nombre impair de flèches pointant vers lui et un nombre pair pointant vers lui, c’est-à-dire
  flèches impaires = flèches paires + 1.
• Transition: Lorsqu’un symbole souhaité est trouvé dans l’entrée, la transition d’un état à un autre état se produit. L’automate passe à l’état suivant ou persiste.
  Une flèche dirigée affiche le mouvement d’un état à un autre tandis qu’une flèche pointe vers l’état de destination.
  Si l’automate reste sur le même état, une flèche pointant d’un état vers lui-même est dessinée.

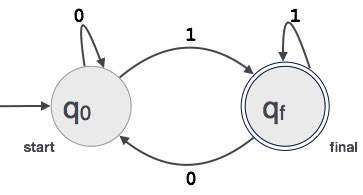
Un exemple; Supposons qu’une valeur binaire à 3 chiffres se terminant par 1 soit acceptée par FA.
Alors FA = {Q(q0, qf), Σ(0,1), q0, qf, δ}

Relation entre les expressions régulières et les automates finis

La relation entre l’expression régulière et les automates finis est la suivante;
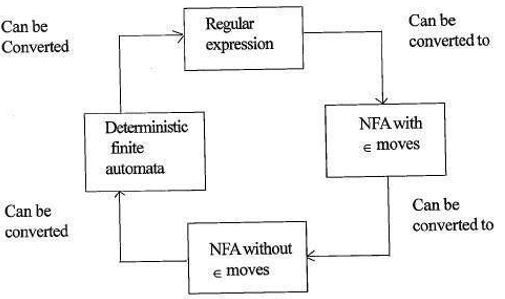
La figure ci-dessous montre qu’il est facile à convertir;

• Expressions régulières vers des automates finis non déterministes (NFA) avec des mouvements ∈.
• Automates finis non déterministes avec ∈ se déplace vers sans ∈ se déplace
• Automates finis non déterministes sans ∈ se déplace vers des Automates Finis Déterministes (DFA).
• Automates finis déterministes à l’expression régulière.

Une Lex acceptera les expressions régulières en entrée et renverra un programme qui simule un automate fini pour reconnaître les expressions régulières.
Par conséquent, lex combinera la génération de motifs de chaînes (expressions régulières définissant les chaînes d’intérêt pour lex) et la reconnaissance de motifs de chaînes (un automate fini qui reconnaît les chaînes d’intérêt).

Règle de correspondance la plus longue

Il indique que le lexème analysé doit être déterminé en fonction de la correspondance la plus longue parmi tous les jetons disponibles.
Ceci est utilisé pour résoudre les ambiguïtés lors de la décision du jeton suivant dans le flux d’entrée.
Lors de l’analyse du code source, l’analyseur lexical analyse le code lettre par lettre et lorsqu’un opérateur, un symbole spécial ou un espace est détecté, il décide si un mot est complet.

Exemple:

int intvalue;

Lors de l’analyse de ce qui précède, l’analyseur ne peut pas déterminer si ‘int’ est un mot clé int ou le préfixe de l’identifiant intvalue.
La priorité de règle est appliquée par laquelle un mot-clé aura la priorité sur l’entrée de l’utilisateur, ce qui signifie que dans l’exemple ci-dessus, l’analyseur générera une erreur.

Erreurs lexicales

Une erreur lexicale se produit lorsqu’une séquence de caractères ne peut pas être analysée dans un jeton valide.
Ces erreurs peuvent être causées par une faute d’orthographe d’identifiants, de mots-clés ou d’opérateurs.
Généralement, bien que des erreurs lexicales très rares soient causées par des caractères illégaux dans un jeton.

Les erreurs peuvent être;

• Erreur d’orthographe.
• Transposition de deux caractères.
• Caractères illégaux.
• Longueur supérieure de l’identifiant ou des constantes numériques.
• Remplacement d’un caractère par un caractère incorrect
• Suppression d’un caractère qui devrait être présent.

La récupération d’erreur implique;

• Suppression d’un caractère de l’entrée restante
• Transposition de deux caractères adjacents
• Suppression d’un caractère de l’entrée restante
• Insertion d’un caractère manquant dans l’entrée restante
• Remplacement d’un caractère par un autre caractère.
• Ignorer les caractères successifs jusqu’à la formation d’un jeton légal (récupération en mode panique).

Schémas de récupération d’erreurs

Récupération en mode panique.
Dans ce schéma de récupération d’erreur, les motifs non appariés sont supprimés de l’entrée restante jusqu’à ce que l’analyseur lexical puisse trouver un jeton bien formé au début de l’entrée restante.
Une mise en œuvre plus facile est un avantage pour cette approche.
Il a la limitation qu’une grande quantité d’entrée est ignorée sans vérifier les erreurs supplémentaires.

Correction locale.
Lorsqu’une erreur est détectée à un point, des opérations d’insertion/suppression et /ou de remplacement sont exécutées jusqu’à ce qu’un texte bien formé soit obtenu.
L’analyseur est redémarré avec le nouveau texte résultant en entrée.

Correction globale.
Il s’agit d’une récupération en mode panique améliorée préférée lorsque la correction locale échoue.
Il a des exigences de temps et d’espace élevées, il n’est donc pas mis en œuvre pratiquement.

Besoin d’analyseurs lexicaux

1. Amélioration de l’efficacité du compilateur – des techniques de mise en mémoire tampon spécialisées pour la lecture des caractères accélèrent le processus du compilateur.
2. Simplicité de conception du compilateur – La suppression des espaces blancs et des commentaires permettra des constructions syntaxiques efficaces pour l’analyseur de syntaxe.
3. Portabilité du compilateur – seul le scanner communique avec le monde extérieur.
4. Spécialisation – des techniques spécialisées peuvent être utilisées pour améliorer le processus d’analyse lexicale

Problèmes liés à l’analyse lexicale

1. Lookahead
   Étant donné une chaîne d’entrée, les caractères sont lus de gauche à droite un par un.
   Pour déterminer si un jeton est terminé ou non, nous devons regarder le caractère suivant.
   Exemple : Est ‘=’ un opérateur d’affectation ou le premier caractère de l’opérateur ‘==’.
   Lookahead ignore les caractères dans l’entrée jusqu’à ce qu’un jeton bien formé soit trouvé, cela montre que look ahead ne peut pas détecter d’erreurs significatives, sauf pour des erreurs simples telles que des symboles illégaux.
2. Ambiguïtés
   Les programmes écrits avec lex acceptent des spécifications ambiguës et choisissent donc la correspondance la plus longue et lorsque plusieurs expressions correspondent à l’entrée, soit la correspondance la plus longue est préférée, soit la première règle parmi les règles correspondantes est priorisée.
3. Mots-clés réservés
   Certains langages ont des mots réservés qui ne sont pas réservés dans d’autres langages de programmation, par exemple elif est un mot réservé en python mais pas en C.
4. Dépendance au contexte
   Exemple:
   Étant donné l’instruction DO 10 l = 10.86, DO10l est un identifiant et DO n’est pas un mot-clé.
   Et étant donné l’instruction DO 10 l = 10, 86, DO est un mot clé
   De telles déclarations nécessiteraient un regard substantiel pour la résolution.

Les applications

1. Utilisées par les compilateurs créent des exécutables binaires conformes à partir de code analysé.
2. Utilisé par les navigateurs Web pour formater et afficher une page Web analysée en HTML, CSS et script java.

Avec cet article chez OpenGenus, vous devez avoir une idée forte de l’Analyse Lexicale dans la Conception du Compilateur.