Diffie-Hellman

Comment deux personnes dans une salle bondée peuvent-elles tirer un secret que seuls les deux connaissent, sans révéler le secret à quiconque pourrait écouter?

C’est exactement le scénario que l’échange de clés Diffie-Hellman existe pour résoudre.

L’échange de clés Diffie-Hellman est un moyen pour deux parties d’établir conjointement un secret partagé sur un canal non sécurisé, sans aucune connaissance préalable l’une de l’autre.

Ils n’échangent jamais réellement le secret, juste quelques valeurs qui se combinent toutes les deux, ce qui leur permet d’atteindre la même valeur résultante.

Conceptuellement, la meilleure façon de visualiser l’échange de clés Diffie-Hellman est avec la démonstration omniprésente de mélange de couleurs de peinture. Il vaut la peine de le revoir rapidement si vous ne le connaissez pas.

Cependant, dans cet article, nous voulons aller plus loin et vous montrer les calculs dans l’échange de clés Diffie-Hellman.

DH Math

Avant d’entrer dans les mathématiques de Diffie-Hellman, vous voudrez avoir une compréhension de base de ce qu’est un nombre premier et de l’opération de module (aka, division du reste). Ces deux termes ont été définis dans un autre article.

Voici une infographie décrivant toutes les étapes de l’échange Diffie-Hellman entre Alice et Bob.

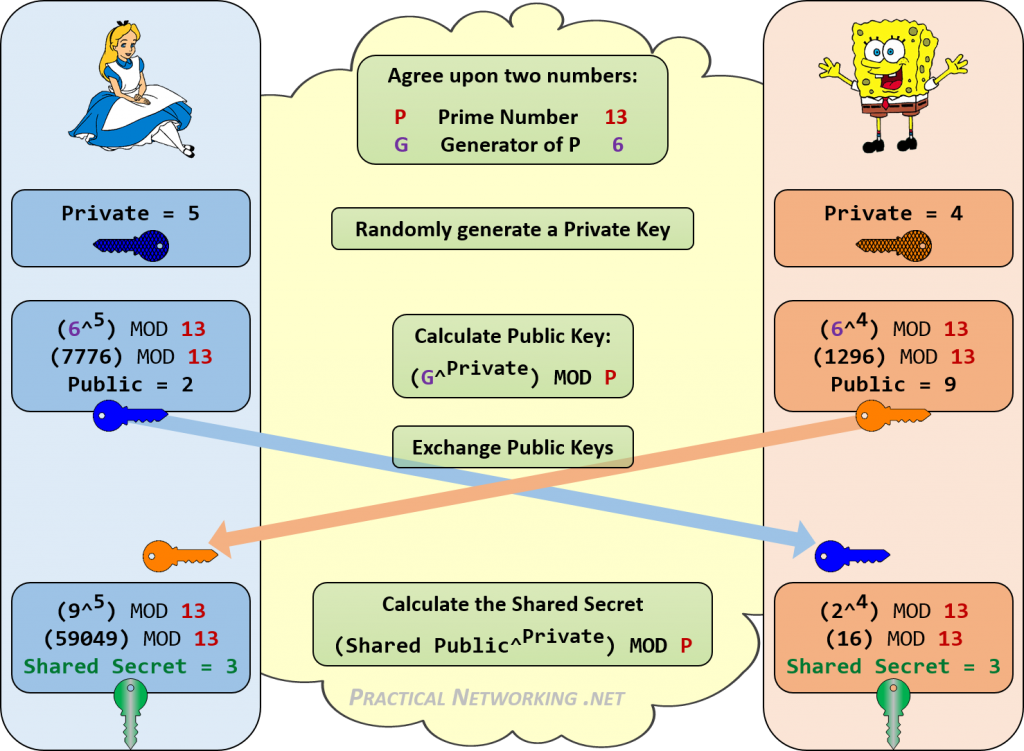
Remarquez comment Alice et Bob ont pu atteindre le même Secret partagé de 3. Quiconque écoute son échange de clés DH ne connaîtrait que les valeurs publiques et les valeurs P et G de départ. Il n’y a pas de moyen cohérent de combiner ces nombres (13, 6, 2, 9) pour atteindre 3.

Nombres DH

Dans notre exemple, nous avons utilisé un nombre premier de 13. Puisque ce nombre premier est également utilisé comme Module pour chaque calcul, l’espace clé entier pour le Secret partagé résultant ne peut jamais être que de 0 à 12. Plus ce nombre est important, plus un attaquant aura du mal à forcer votre secret partagé.

Évidemment, nous utilisions de très petits nombres ci-dessus pour aider à garder le calcul relativement simple. Les vrais échanges DH font des calculs sur des nombres beaucoup plus grands. Il y a trois tailles typiques aux nombres dans Diffie-Hellman:

La taille des bits est une référence au nombre premier. Cela équivaut directement à tout l’espace clé du Secret partagé résultant. Pour vous donner une idée de la taille de cet espace clé:

Pour écrire complètement un nombre de 768 bits, vous auriez besoin de 232 chiffres décimaux.
Pour écrire complètement un nombre de 1024 bits, vous auriez besoin de 309 chiffres décimaux.
Pour écrire complètement un nombre de 1536 bits, vous auriez besoin de 463 chiffres décimaux.

En utilisant le Secret Partagé

Une fois le Secret Partagé atteint, il est généralement utilisé dans le calcul pour établir une clé de chiffrement Symétrique conjointe et/ ou une Clé HMAC conjointe – également appelée Clés de session.

Mais il est important de souligner que le Secret partagé lui-même ne doit pas être directement utilisé comme clé secrète. Si c’était le cas, tout ce dont vous pouvez être assuré, c’est que tout au long de la conversation sécurisée, vous parlez toujours à la même partie qui était de l’autre côté de l’échange Diffie-Hellman.

Cependant, vous n’avez toujours aucune confirmation ou assurance quant à l’identité de l’autre partie. Juste que personne d’autre ne peut tout d’un coup prétendre être eux au milieu de votre conversation sécurisée.

La génération des clés de session réelles doit inclure le secret partagé DH, ainsi qu’une autre valeur qui ne serait connue que de l’autre partie prévue, comme quelque chose du schéma d’authentification que vous avez choisi.

Préférez le contenu vidéo au texte? La majorité de cet article a été enregistrée et peut être visionnée sur Youtube:

Exemple de navigation de la série RSA > >