Quelles Formules Mathématiques ACT Les Élèves Doivent-Ils Connaître et Conseils Pour Les Mémoriser?
La section de mathématiques ACT comprend 60 questions à cinq choix multiples auxquelles les élèves doivent répondre dans les 60 minutes. Les questions sont tirées de six domaines thématiques couverts jusqu’à la 11e année. Ils comprennent la pré-algèbre, l’algèbre intermédiaire, l’algèbre élémentaire, la géométrie des coordonnées, la trigonométrie et la géométrie plane.
Voici les sujets et compétences abordés lors du test de Maths ACT.
Algèbre
La section comprend 14 questions et teste l’étudiant sur les décimales, les nombres entiers, les fractions, le rapport, les puissances entières positives, les entiers, les racines carrées, le pourcentage et la proportion. Les autres sujets testés incluent une variable, les équations linéaires, la valeur absolue, les multiples et facteurs, la médiane, la moyenne, le mode, l’interprétation des données et les problèmes et probabilités de comptage.
Algèbre intermédiaire
Cette partie comprend neuf questions testant l’étudiant en inégalités, valeur absolue, formule quadratique, systèmes d’équations, expressions rationnelles et radicales, fonctions, inégalités quadratiques, polynômes, matrices et nombres complexes.
Algèbre élémentaire
Il y aura une dizaine de questions dans le domaine touchant les polynômes, les variables, la factorisation, les exposants entiers, les racines carrées, les inégalités linéaires et les équations quadratiques.
Géométrie plane
Vous aurez 14 questions touchant des figures planes telles que des rectangles, des parallélogrammes, des triangles, des trapèzes et des cercles. Certaines questions testent les connaissances sur les lignes perpendiculaires, les rotations, la géométrie 3D, l’aire, le périmètre, le raisonnement logique, le volume, les translations et les réflexions.
Géométrie des coordonnées
Il y aura environ neuf questions du test d’aire sur le graphique des points, des graphes linéaires numériques, des cercles, des polynômes, des lignes, des courbes, une formule de point médian, des coniques, des transformations, une formule de distance, des équations et des relations de graphe, la pente et les propriétés des lignes perpendiculaires et parallèles.
Dans la section, la trigonométrie trouvera quatre questions sur les fonctions trigonométriques, les équations et les identités, les rapports trigonométriques en triangle rectangle et la modélisation des fonctions trigonométriques.
Liste des formules mathématiques ACT
Voici une liste de 13 formules mathématiques ACT que vous devez connaître pour le test ACT:
- Moyenne arithmétique
- Probabilité
- Équation Quadratique
- Formule de Distance
- Formule de Pente
- Formule d’Interception de pente
- Formule de Point milieu
- Aire d’un Triangle
- Théorème de Pythagore
- Aire du Rectangle et du Périmètre
- Volume du Cuboïde
- Aire d’un Cercle
- Formules trigonométriques
Moyenne arithmétique
C’est la même chose que la moyenne, et c’est la somme de tous les articles divisés par le nombre d’articles. Par exemple, en calculant la moyenne des valeurs, vous avez divisé la somme par le nombre de valeurs
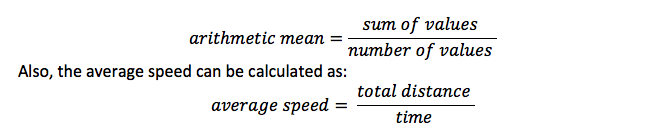
Formule de probabilité
La probabilité est utilisée pour calculer la possibilité du nombre de fois où quelque chose se produira dans un ensemble de résultats possibles. C’est une représentation des chances que quelque chose se passe. Une probabilité de 1 signifie qu’il y a quelque chose en particulier qui se produira, mais une possibilité de 0 signifie que quelque chose ne se produira pas.
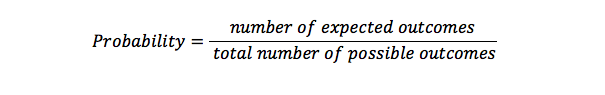
Équation quadratique
La formule exprimée par:
x = -b ± √b2-4ac/2a
Il est utilisé pour déterminer les interceptions x d’une équation parabolique ou quadratique.
Formule de distance
La formule est utilisée pour calculer la distance entre deux points d’un plan de coordonnées. La formule est exprimée comme suit:
d = √(x₁–x₂) 2 + ²y₁-y₂) 2
Formule de pente
La pente est une mesure des changements de ligne exprimés en tant que changement d’axe des ordonnées divisé par le changement sur l’axe des abscisses (montée / course).
Par exemple, si vous avez le point A(X1, Y1) et B(X2, Y2), vous pouvez calculer la pente comme suit:
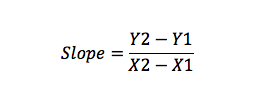
Formule d’interception de pente
La formule d’interception de pente est une équation linéaire exprimée en Y = MX + b dans laquelle:
- M représente la pente de la droite, tandis que b est l’ordonnée à l’origine où le point d’interception y croise l’axe Y.
- Si la droite traverse l’origine, l’ordonnée à l’origine est nulle et l’équation sera exprimée par Y = MX.
Formule du point médian
Il s’agit d’une formule qui trouve le point médian d’une ligne. Par exemple, si vous avez deux points, A(X1, Y1) et B(X2, Y2), le point médian sera:
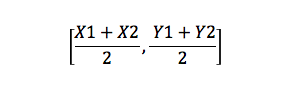
Aire d’un triangle
La formule exprimée en ½ (hauteur de base x) est utilisée pour calculer l’aire totale enfermée dans un triangle.
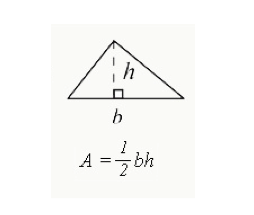
- b = la base du triangle (le bord d’un côté)
- h = la hauteur d’un triangle. La hauteur pour un triangle à angle droit sera le côté avec un angle de 90 degrés. Pour les autres triangles, la hauteur descend à l’intérieur du triangle, comme indiqué ci-dessus.
Théorème de Pythagore
Le théorème de Pythagore est crucial lors du calcul du côté inconnu d’un triangle rectangle lorsque deux côtés sont connus. La formule est exprimée par a2 + b2 = c2. La somme de deux côtés plus courts est égale à la somme du côté le plus long.

Zone du Rectangle et du Périmètre
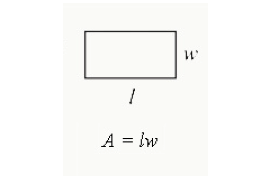
Pour trouver l’aire d’un rectangle, vous multipliez la longueur par la largeur. C’est la surface totale enfermée dans un rectangle.
Area = Longueur x Largeur
D’autre part, le périmètre d’un rectangle est la distance qui l’entoure.
Périmètre = (L+ W + L+ W) simplifié en 2 (L + W)
Volume de Cuboïde
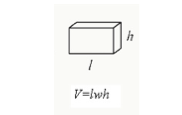
Vous pouvez calculer le volume d’un cuboïde en multipliant sa longueur, sa largeur et sa hauteur.
Aire d’un cercle
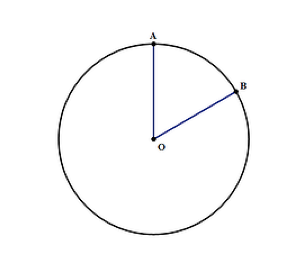
L’aire d’un cercle peut être trouvée en utilisant la formule nr2 où:
- π est une constante qui s’écrit 3.14, ce qui est important à retenir si vous n’aurez pas de calculatrice pendant le test
- r – est le rayon du cercle, comme dans le diagramme ci-dessus. C’est la distance de O au bord du cercle au point A ou B
de même, la distance autour du cercle est appelée circonférence. Il est calculé comme suit:
Circonférence du cercle = nD ou 2nr
Où:
- D, qui est le diamètre est deux fois le rayon du cercle. C’est la ligne qui divise le cercle en deux demi touchant deux extrémités d’un cercle.
Formules trigonométriques Sinus (SOH), Cosinus (CAH), Tangente (TOA)
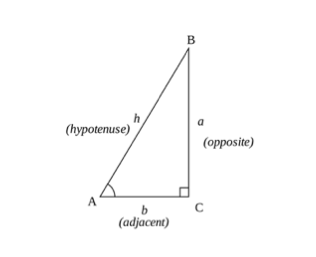
Les calculs trigonométriques peuvent être additionnés par des concepts de base d’un triangle en utilisant les règles sinus, cosinus et tangente (SOHCAHTOA). Vous pouvez calculer le cosinus, le sinus ou la tangente d’un angle en utilisant les côtés d’un triangle.

Où:
- Côté opposé – est le côté du triangle opposé à l’angle ()
- Côté adjacent – est le côté le plus proche de l’angle mais pas le côté le plus long.
- L’hypoténuse est le côté le plus long du triangle.
Conseils pour Mémoriser les Formules et équations de mathématiques ACT
Pour mémoriser les formules lors de l’examen ACT, il est important de se familiariser tôt en lisant dans les domaines de sujet spécifiés pour le test de mathématiques.
Vous pouvez également vous entraîner en essayant autant de problèmes que possible pour maîtriser la formule.
Utiliser différents canaux comme dire les formules plus fort ou les écrire sur des graphiques et les coller dans votre pièce peut vous aider à vous souvenir des formules.