ACT matematikai képletek

milyen ACT matematikai képleteket kell tudniuk a hallgatóknak, és tippeket kell megjegyezniük?

az ACT Math szakasz 60 öt feleletválasztós kérdést tartalmaz, amelyekre a hallgatóknak 60 percen belül válaszolniuk kell. A kérdéseket hat, a 11. osztályig terjedő témakörből vonják le. Ezek közé tartozik a Pre-algebra, a köztes algebra, az elemi algebra, a Koordináta geometria, a trigonometria és a sík geometria.

itt találhatók a Math ACT teszt témái és készségei.

Algebra

a szakasz 14 kérdést tartalmaz, és teszteli a hallgatót tizedesjegyekkel, egész számokkal, törtekkel, arányokkal, pozitív egész hatványokkal, egészekkel, négyzetgyökekkel, százalékkal és arányokkal. Egyéb vizsgált témák közé tartozik egy változó, lineáris egyenletek, abszolút érték, többszörösei és tényezői, medián, átlag, mód, adatok értelmezése, és számlálási problémák és valószínűség.

köztes Algebra

ez a rész kilenc kérdést tartalmaz, amelyek a hallgatót egyenlőtlenségekben, abszolút értékekben, másodfokú képletben, egyenletrendszerekben, racionális és radikális kifejezésekben, függvényekben, másodfokú egyenlőtlenségekben, polinomokban, mátrixokban és komplex számokban tesztelik.

elemi Algebra

körülbelül tíz kérdés lesz a területen, amelyek érintik a polinomokat, a változókat, a faktoringot, az egész kitevőket, a négyzetgyökeket, a lineáris egyenlőtlenségeket és a másodfokú egyenleteket.

sík geometria

lesz 14 kérdés érintő sík számok, mint a téglalapok, paralelogrammák, háromszögek, trapéz, körök. Néhány kérdés merőleges vonalakon, forgatásokon, 3D geometrián, területen, kerületen, logikai érvelésen, köteten, fordításokon és reflexiókon teszteli a tudást.

Koordináta geometria

lesz körül kilenc kérdést a terület tesztelés a grafikonon pontok, számvonal grafikonok, körök, polinomok, vonalak, görbék, középponti képlet, conics, transzformációk, távolság formula, egyenletek és gráf kapcsolatok, meredekség, és tulajdonságai merőleges és párhuzamos vonalak.

ebben a szakaszban a trigonometria négy kérdést talál a trigonometrikus függvényekről, egyenletekről és identitásokról, a derékszögű háromszög trigonometrikus arányairól és a trigonometrikus függvények modellezéséről.

az ACT matematikai képletek listája

itt van egy lista a 13 ACT matematikai képletről, amelyet tudnia kell az ACT teszthez:

1. számtani átlag
2. valószínűség
3. másodfokú egyenlet
4. távolság képlet
5. lejtő képlet
6. lejtő Metszésképlete
7. középpont képlet
8. háromszög területe
9. Pitagorasz-tétel
10. terület téglalap és kerülete
11. térfogata kockás
12. terület egy kör
13. trigonometrikus képletek

számtani átlag

ez ugyanaz, mint az átlagos, és ez az összeg a minden elem osztva az elemek számával. Például az értékek átlagának kiszámításakor az összeget elosztjuk az értékek számával

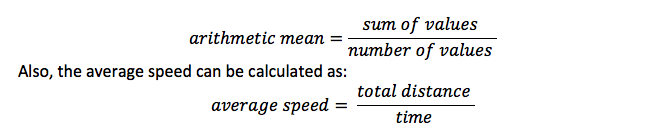
valószínűségi képlet

a valószínűséget arra használjuk, hogy kiszámítsuk annak lehetőségét, hogy hányszor fordul elő valami a lehetséges eredmények halmazában. Ez annak az esélye, hogy valami történik. Az 1 valószínűsége azt jelenti, hogy van valami, ami meg fog történni, de a 0 lehetősége azt jelenti, hogy valami nem fog megtörténni.

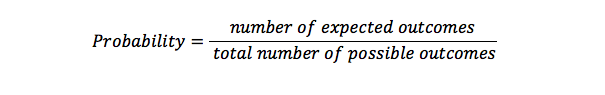
másodfokú egyenlet

a képlet kifejezve:

x = −B B2-4ac/2a

parabolikus vagy másodfokú egyenlet x-elfogásainak meghatározására szolgál.

távolság képlet

a képletet a koordinátasík két pontja közötti távolság kiszámításakor használják. A képletet a következőképpen fejezzük ki:

d=ons (Xi-x₂) 2 + (yi – y₂)2

meredekség képlet

a meredekség az Y tengely változásaként kifejezett vonalváltozások mértéke oszd meg az X tengely változásával (emelkedés/futás).

például, ha van a (X1, Y1) és B(X2, Y2) pontja, akkor kiszámíthatja a meredekséget:

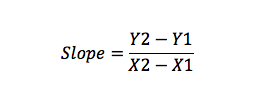
Slope Intercept Formula

a slope-intercept formula egy egyenlet, amelyet y=MX+b-ben fejeznek ki:

• M a vonal meredekségét jelenti, míg b az y-metszéspont, ahol az y-metszéspont keresztezi az y tengelyt.
• ha a vonal áthalad az Origón, akkor az y-metszéspont nulla, és az egyenlet Y=MX-ként lesz kifejezve.

középpont képlet

ez egy olyan képlet, amely megtalálja a vonal középpontját. Például, ha két pontod van, A (X1, Y1) és B (X2, Y2), akkor a középpont a következő lesz:

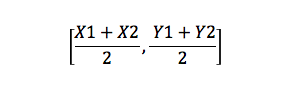
a háromszög területe

A (Z) – ban kifejezett képletet (alap x magasság) használjuk a háromszögbe zárt teljes terület kiszámításához.

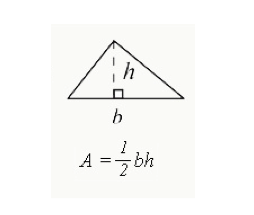
• b= a háromszög alapja (az egyik oldal széle)
• h=egy háromszög magassága. A derékszögű háromszög magassága 90 fokos szögű oldal lesz. Más háromszögek esetében a magasság leesik a háromszög belsejéből, amint az fent látható.

Pitagorasz-tétel

Pitagorasz-tétel döntő fontosságú a derékszögű háromszög ismeretlen oldalának kiszámításakor, ha két oldala ismert. A képletet A2+b2=c2-ben fejezzük ki. Két rövidebb oldal összege megegyezik a hosszabb oldal összegével.

a téglalap és a kerület területe

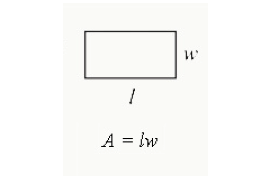
a téglalap területének megkereséséhez szorozza meg a hosszúságot a szélességgel. Ez a téglalapba zárt teljes terület.

terület = hossz x szélesség

másrészt egy téglalap kerülete a körülötte lévő távolság.

Perimeter = (L+W+L+W) egyszerűsítve 2 (L + W)

a téglatest térfogata

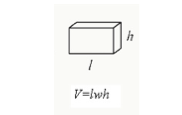
kiszámíthatja a kocka térfogatát úgy, hogy megszorozza annak hosszát, szélességét és magasságát.

egy kör területe

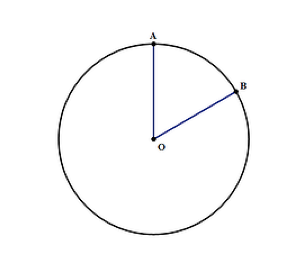
egy kör területe megtalálható az Nr2 képlet segítségével, ahol:

• az a konstans, amit 3-nak írunk.14, ami fontos megjegyezni, ha nem lesz számológéped a teszt során
• r-a kör sugara, mint a fenti ábrán. Ez a Távolság O-tól a kör széléig az A vagy B pontban

hasonlóképpen, a kör körüli távolságot kerületnek nevezzük. Kiszámítása:

a kör kerülete = nD vagy 2NR

ahol:

• D, ami az átmérő kétszerese a kör sugara. Ez az a vonal, amely a kört két felére osztja, megérintve a kör két végét.

trigonometrikus képletek szinusz (SOH), koszinusz (CAH), érintő (TOA)

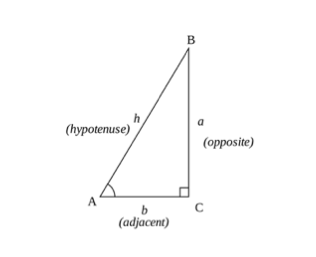
a trigonometrikus számításokat egy háromszög alapfogalmaival lehet összefoglalni a szinusz, koszinusz és érintő szabályok (SOHCAHTOA) felhasználásával. A szög koszinuszát, szinuszát vagy érintőjét háromszög oldalai segítségével kiszámíthatja.

ahol:

• ellentétes oldal – a háromszög szögével ellentétes oldala ()
• szomszédos oldal – a szöghez legközelebb eső, de nem a leghosszabb oldal.
• a hipotenusz a háromszög leghosszabb oldala.

tippek az ACT matematikai képletek és egyenletek memorizálásához

az ACT vizsga során a képletek memorizálásához fontos, hogy korán megismerkedjen a matematikai teszthez megadott témakörök olvasásával.

azt is gyakorolni próbál annyi problémát, mint lehetséges, hogy elsajátítsák a képlet.

különböző csatornák használata, mint például a képletek hangosabb kimondása vagy a diagramokra írása és a szobájába ragasztása, segíthet emlékezni a képletekre.