Diffie-Hellman

hogyan lehet két ember egy zsúfolt szobában levezetni egy titkot, amelyet csak a pár tud, anélkül, hogy felfedné a titkot bárki másnak, aki esetleg hallgat?

pontosan ez a forgatókönyv a Diffie-Hellman KULCSCSERE létezik megoldani.

a Diffie-Hellman KULCSCSERE egy eszköz arra, hogy két fél közösen hozzon létre egy közös titkot egy nem biztonságos csatornán keresztül, anélkül, hogy előzetesen ismernék egymást.

valójában soha nem cserélik ki a titkot, csak néhány olyan értéket, amelyek együttesen lehetővé teszik számukra, hogy ugyanazt az eredményt érjék el.

fogalmilag a Diffie-Hellman KULCSCSERE vizualizálásának legjobb módja a mindenütt jelenlévő festékszínkeverési bemutató. Érdemes gyorsan áttekinteni, ha nem ismeri.

ebben a cikkben azonban egy lépéssel tovább akarunk menni, és ténylegesen megmutatjuk a matematikát a Diffie-Hellman Kulcscserében.

DH Math

mielőtt Belemennél a Diffie-Hellman matematikájába, alaposan meg kell értened, hogy mi a prímszám, és mi a Modulus művelet (más néven fennmaradó Osztás). Mindkét kifejezést egy másik cikk határozta meg.

az alábbiakban egy infografika ismerteti az Alice és Bob közötti Diffie-Hellman csere lépéseit.

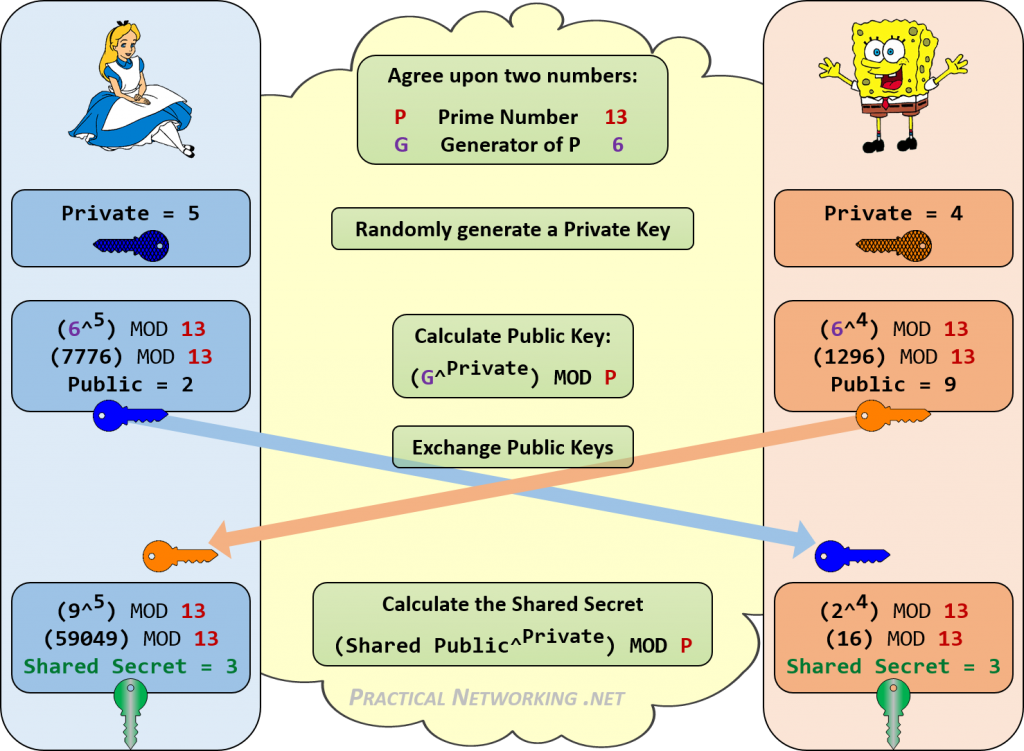
figyeljük meg, hogy Alice és Bob hogyan tudták elérni ugyanazt a közös 3-as titkot. Bárki, aki hallgatja a DH Kulcscseréjét, csak a nyilvános értékeket ismeri, valamint a kezdő P és G értékeket. Nincs következetes módja annak, hogy ezeket a számokat (13, 6, 2, 9) kombináljuk a 3 eléréséhez.

DH számok

példánkban 13-as prímszámot használtunk. Mivel ezt a prímszámot is használják Modulusként az egyes számításokhoz, a kapott megosztott titok teljes kulcsterülete csak 0-12 lehet. Minél nagyobb ez a szám, annál nehezebb idő lesz a támadónak brute kényszerítve a megosztott titkot.

nyilvánvaló, hogy a fenti nagyon kis számokat használtuk, hogy a matematika viszonylag egyszerű legyen. Igaz DH cserék csinálnak matematikai számok, amelyek mérhetetlenül nagyobb. A Diffie-Hellman számoknak három tipikus mérete van:

a bitméret a Prímszámra való hivatkozás. Ez közvetlenül megegyezik a kapott megosztott titok teljes kulcsterületével. Ahhoz, hogy képet kapjon arról, hogy mekkora ez a kulcsterület:

a 768 bites szám teljes kiírásához 232 decimális számjegy szükséges.
az 1024 bites szám teljes kiírásához 309 decimális számjegy szükséges.
az 1536 bites szám teljes kiírásához 463 decimális számjegy szükséges.

a megosztott titok használata

a megosztott titok elérése után általában a számítás során használják egy közös szimmetrikus titkosítási kulcs és/vagy egy közös HMAC kulcs – más néven munkamenet kulcsok.

de fontos kiemelni, hogy maga a megosztott titok nem használható közvetlenül titkos kulcsként. Ha így lenne, csak abban lehet biztos, hogy a biztonságos beszélgetés során továbbra is ugyanazzal a féllel beszél, amely a Diffie-Hellman csere másik oldalán volt.

azonban még mindig nincs megerősítés vagy biztosíték arra vonatkozóan, hogy ki a másik fél. Csak azt, hogy senki más hirtelen úgy tesz, mintha ők lennének a biztonságos beszélgetés közepén.

a tényleges Munkamenetkulcsok generálásának tartalmaznia kell a DH megosztott titkot, valamint néhány más értéket, amelyet csak a kívánt másik fél ismer, például valamit a választott hitelesítési sémából.

a videotartalmat részesíti előnyben a szöveg helyett? A cikk nagy részét rögzítették, és megtekinthető a Youtube-on:

sorozat navigációs RSA példa > >