線形膨張率、面積膨張率、体積または立方膨張率はすべて熱エネルギーによって支配されているパラメータです。 すべての3つのパラメータは、温度の摂氏単位で主にある温度上昇に依存しています。
線形膨張率は元の長さと最終長さにさらに依存し、面積膨張率は元の面積と最終面積にさらに依存し、最後に立方または体積膨張率は元の体積と最終
線形膨張率を計算するための式は、(l2–l1)/l1≤
l2は最終的な長さを表します。
l1は元の長さを表します。
θは摂氏での温度上昇を表します。
面積膨張率の計算式は、(A2–A1)/A1≤
A2は最終的な面積を表します。
A1は元の領域を表します。
θは摂氏での温度上昇を表します。
体積または立方膨張率を計算する式は、(V2–V1)/V1≤
V2は最終体積を表します。
v1は元のボリュームを表します。
θは摂氏での温度上昇を表します。
線形膨張率、面積膨張率、体積または立方膨張率の三つの例をそれぞれ解いてみましょう。 電卓百科事典(Nickzom電卓)は、式の仕組みを示すこれらのパラメータを解決し、正確に答えることができます。
まず第一に、これらの手段のいずれかを介してNickzom電卓にアクセスする必要があります:
- ウェブ– https://www.nickzom.org/calculator-plus
- アンドロイド(有料)) – https://play.google.com/store/apps/details?id=org.nickzom.nickzomcalculator
- アップル(有料) – https://itunes.apple.com/us/app/nickzom-calculator/id1331162702?mt=8
次に、計算機マップに進み、物理セクションの下の熱エネルギーをクリックします
例1:
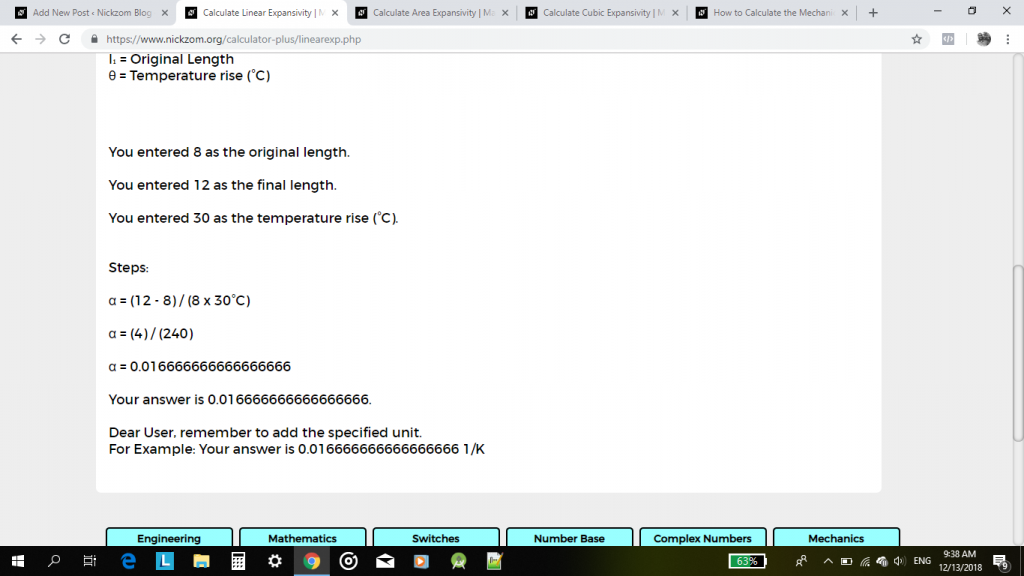
20℃の温度上昇を受けた後、元の長さが8cm、最終長さが12cmの金属の線形膨張率(α)を求めます。
α=(l2–l1)/l1≤
ここで、
α=(l2-l1)/l1≤
:<3 1 0>l2(最終長さ)=1 2cm<3 1 0>l1(元の長さ)=8cm<3 1 0>λ(温度上昇)=2 0℃<1 2 3 2><6 4 8>したがって、<1 2 3 2><6 4 8>α(最終長さ)=1 2cm<3 1 0>l1(元の長さ)=8cm<3 1 0>λ(温度上昇)=2 0℃<1 2 3 2><6 4 8>α(温度上昇)=1 2cm<1 2 3 2><= (12 – 8) / 8(20) 1/°C
α=4 / 160 1/°c
α=0.025 1/°C
Nickzom計算機を使用して、線形Expansivityをクリックします,
次に、値を適切かつ正確に入力します
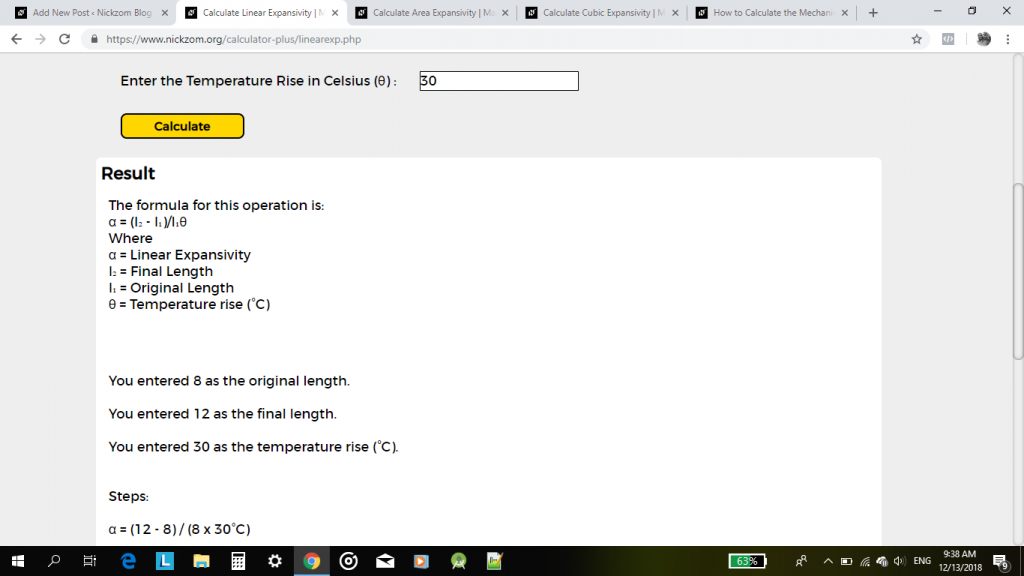
最後に、計算ボタンをクリックします
例2:
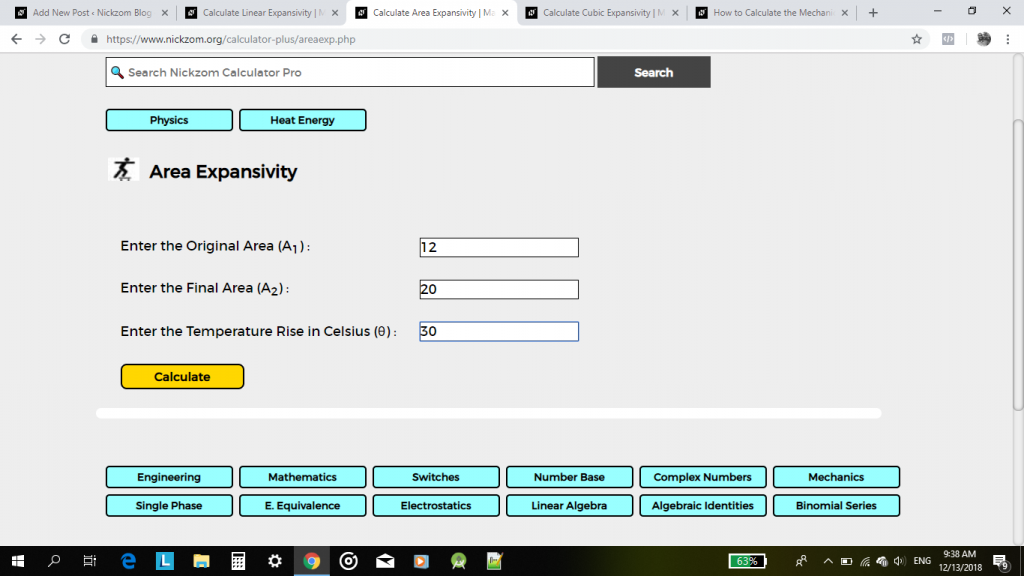
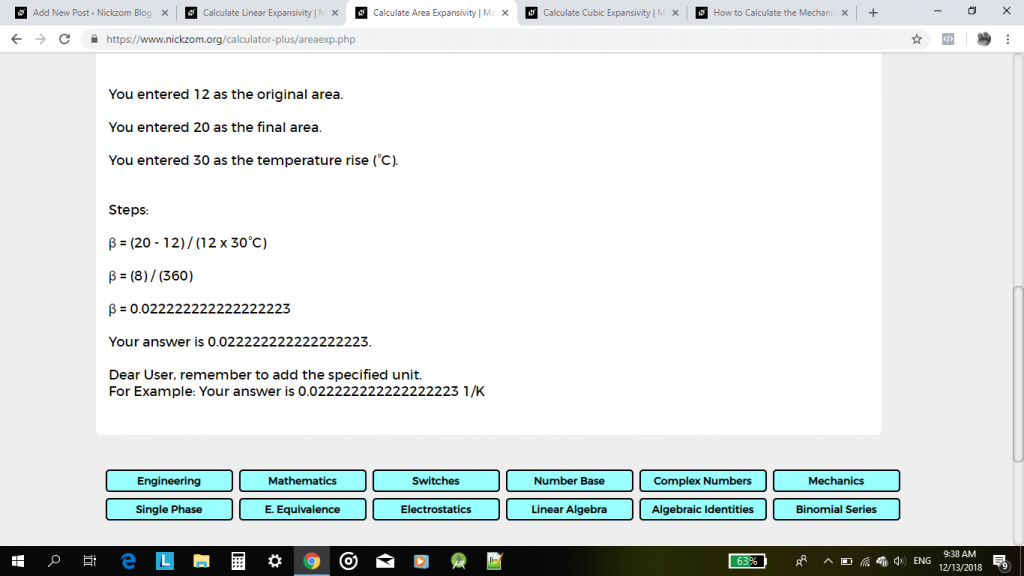
30℃の温度上昇後、元の面積が12cm2、最終長さが20cm2の金属の面積膨張率(β)を求めます。
β=(A2–A1)/A1≤
ここで、
A2(最終面積)=20cm2
A1(元面積)=12cm2
≤(温度上昇)=30℃
したがって、
β= (20 – 12) / 12(30) 1/°C
β=8 / 360 1/°C
β=0.02222-1232-648,

次に、値を適切かつ正確に入力します
最後に、計算ボタンをクリックします

例3:
50℃の温度上昇後、元の体積が18cm3、最終長さが30cm3の金属の体積または立方膨張率(λ)を求めます。
λ=(V2–V1)/V1Λ
ここで、
λ=(V2-V1)/V1Λ
:
v2(最終体積)=18cm3
v1(元体積)=30cm3
λ(温度上昇)=50°C
したがって、