ACT数学の公式

学生が知っておくべきACT数学の公式とそれらを暗記す

ACT数学セクションは、学生が60分以内に応答する必要があります60五つのマルチ選択肢の質問で構成されています。 質問は11年生までカバー六つのトピック領域から引き出されています。 それらには、前代数、中間代数、初等代数、座標幾何学、三角法、および平面幾何学が含まれる。

ここでは、数学行為テストでカバーされているトピックとスキルがあります。

代数

セクションでは、14の質問で構成され、小数、整数、分数、比率、正の整数のべき乗、整数、平方根、パーセンテージ、および割合について学生をテストします。 テストされた他のトピックには、一つの変数、線形方程式、絶対値、倍数と因子、中央値、平均値、モード、データ解釈、およびカウント問題と確率が含まれます。

中間代数

この部分は、不等式、絶対値、二次式、方程式のシステム、有理式とラジカル式、関数、二次不等式、多項式、行列、複素数で学生をテストする九

初等代数

多項式、変数、因数分解、整数指数、平方根、線形不等式、および二次方程式に触れる領域には約10の質問があります。

平面形状

長方形、平行四辺形、三角形、台形、円などの平面図形に触れる14の質問があります。 いくつかの質問は、垂直線、回転、3次元幾何学、面積、周囲、論理的推論、体積、平行移動、および反射に関する知識をテストします。

座標幾何学

点のグラフ、数折れ線グラフ、円、多項式、線、曲線、中点式、円錐、変換、距離式、方程式、グラフの関係、傾き、垂直線と平行線の特性についての領域テストから約9つの質問があります。

セクションでは、三角法は、三角関数、方程式と恒等式、直角三角形の三角比、および三角関数モデリングに関する四つの質問を見つけるでしょう。

ACTの数学の数式のリスト

ここでは、ACTテストのために知っておく必要がある13ACTの数学の数式のリストです:

1. 算術平均
2. 確率
3. 二次方程式
4. 距離式
5. 勾配式
6. 勾配切片式
7. 中点式
8. 三角形の面積
9. ピタゴラスの定理
10. 長方形と周囲の面積
11. 直方体の体積
12. 円の面積
13. 三角法の公式

算術平均

これは平均と同じであり、すべてのアイテムをアイテムの数で割ったもの。 たとえば、値の平均を計算すると、合計を値の数で割った

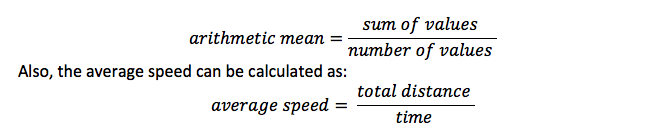
確率式

確率は、可能な結果のセットで何かが発生する回数の可能性を計算する それは何かが起こっている可能性を表しています。 1の確率は、起こる特定の何かがあることを意味しますが、0の可能性は何かが起こらないことを意味します。

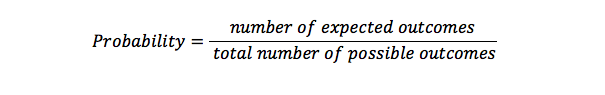
二次方程式

次のように表される式:

x=−b±√b2-4ac/2a

放物線方程式または二次方程式のx切片を決定するために使用されます。

距離式

座標平面上の二つの点間の距離を計算するときに使用されます。 式は次のように表されます。

d=π(x≤–x≤)2+(y≤–y≤)2

傾き式

傾きは、Y軸の変化をX軸の変化（立ち上がり/実行）で割ったものとして表される線の変化の尺度です。たとえば、点A（X1、Y1）とB（X2、Y2）がある場合、勾配は次のように計算できます:

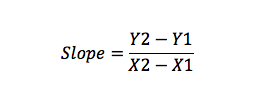
スロープ切片式

スロープ切片式は、Y=MX+bで表される線方程式です。:

• Mは線の傾きを表し、bはy切片点がy軸と交差するy切片です。
• 線が原点を通過する場合、y切片はゼロであり、方程式はY=MXで表されます。

中点式

これは、線の中点を見つける式です。 たとえば、A（X1、Y1）とB（X2、Y2）の2つの点がある場合、中点は次のようになります:

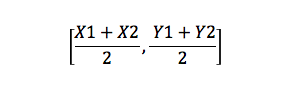
三角形の面積

三角形に囲まれた総面積を計算するには、θ（底x高さ）で表される式を使用します。

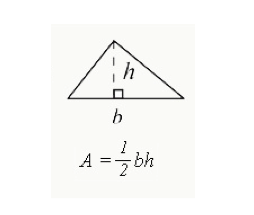
• b=三角形の底辺（一方の辺の端）
• h=三角形の高さ。 直角三角形の高さは、90度の角度を持つ辺になります。 他の三角形の場合、上に示したように、高さは三角形の内部をドロップダウンします。

ピタゴラスの定理

ピタゴラスの定理は、二つの辺がわかっているときに直角三角形の未知の辺を計算するときに重要です。 式はa2+b2=c2として表されます。 二つの短い辺の合計は、長い辺の合計に等しいです。

長方形および周囲の区域

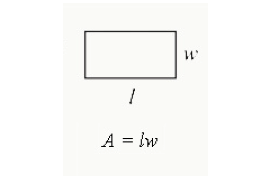
長方形の面積を見つけるには、長さに幅を掛けます。 これは、長方形で囲まれた総面積です。

面積=長さx幅

一方、長方形の周囲はその周りの距離です。

周囲=(L+W+L+W)を2(L+W)として単純化した

直方体の体積

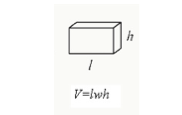
直方体の長さ、幅、および高さを乗算することで、直方体の体積を計算できます。

円の面積

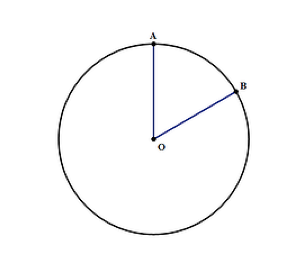
円の面積は、式nr2を使用して見つけることができます。:

• λは3と書かれる定数である。図14に示すように、テスト中に電卓がないかどうかを覚えておくことが重要です
• r-は、上の図のように円の半径です。 これは、点AまたはBにおけるOから円の端までの距離である

同様に、円の周りの距離を円周と呼びます。 それは次のように計算されます。

円の円周=nDまたは2nr

ここで、:

• 直径であるDは、円の半径の2倍です。 これは、円の両端に触れる2つの半分に円を分割する線です。

三角法式正弦(SOH)、余弦(CAH)、正接(TOA))

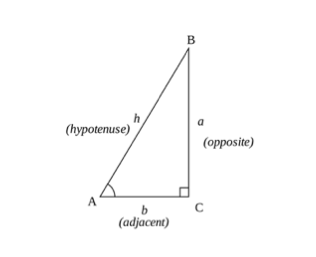
三角法の計算は、正弦、余弦、および接線の規則（SOHCAHTOA）を使用して三角形の基本的な概念によって合計することができます。 三角形の辺を使用して、角度の余弦、正弦、または正接を計算できます。

どこで:

• 反対側-角度と反対側の三角形の辺です()
• 隣接する辺-角度に最も近い辺ですが、最長の辺ではありません。
• 斜辺は三角形の最長辺です。

ACT数学の数式と方程式を暗記するためのヒント

ACT試験中に数式を暗記するには、数学のテストのために指定されたトピック領域を読んで、早期に

数式をマスターするために、できるだけ多くの問題を試みることによって練習することもできます。

数式を大声で言ったり、チャートに書いたり、部屋に貼り付けたりするなど、さまざまなチャンネルを使用すると、数式を覚えやすくなります。