Diffie-Hellman

混雑した部屋の二人は、聞いているかもしれない他の誰にも秘密を明らかにすることなく、ペアだけが知っている秘密をどのように導き出すこ

それはまさにDiffie-Hellman鍵交換が解決するために存在するシナリオです。

Diffie-Hellman鍵交換は、お互いの事前の知識を持たずに、安全でないチャネルを介して共有秘密を共同で確立するための手段です。

彼らは実際には秘密を交換することはなく、両方が結合して同じ結果の値を達成できるいくつかの値だけを交換します。

概念的には、Diffie-Hellmanキー交換を視覚化する最良の方法は、ユビキタスなペイント色混合デモを使用することです。 あなたがそれに慣れていない場合は、すぐにそれを見直す価値があります。

しかし、この記事ではさらに一歩進んで、実際にDiffie-Hellman鍵交換の数学を紹介したいと思います。Diffie-Hellmanの数学に入る前に、素数が何であるか、そしてモジュラス演算が何であるか（別名、剰余除算）の基本的な理解をしたいと思うでしょう。 これらの用語の両方は、別の記事で定義されています。

以下は、AliceとBobの間のDiffie-Hellman交換のすべてのステップを概説したインフォグラフィックです。

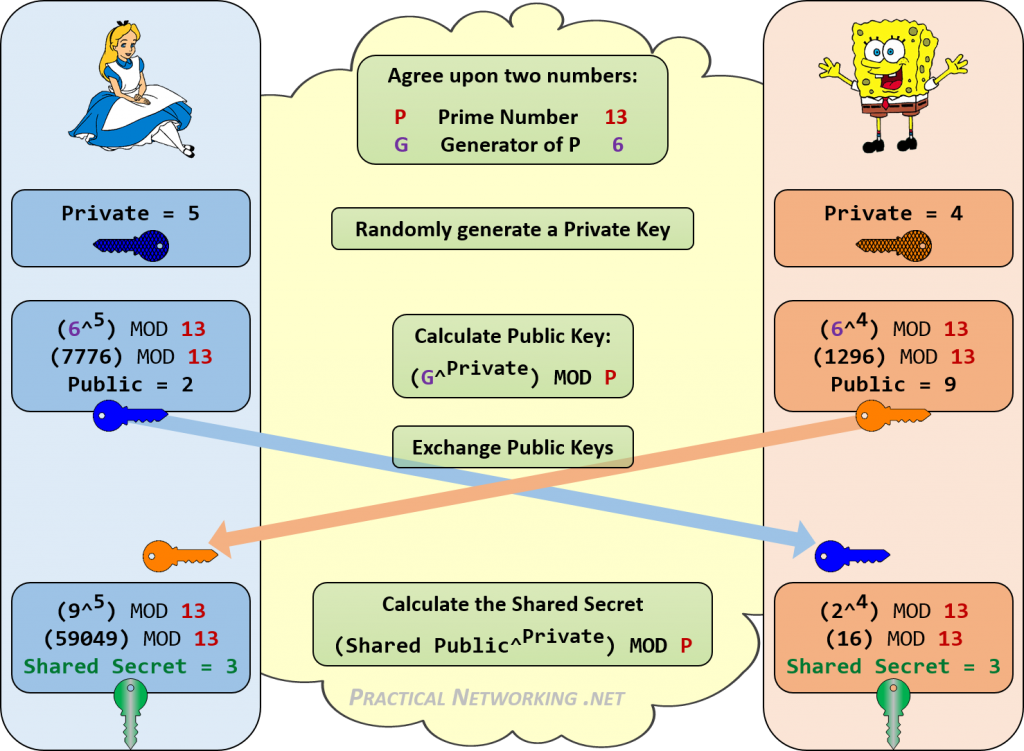
AliceとBobの両方が3の同じ共有秘密を達成することができたことに注意してください。 DHキー交換を聞いている人は、公開値と開始P値とG値のみを知っています。 これらの数字（13、6、2、9）を組み合わせて3を達成する一貫した方法はありません。この例では、13の素数を使用しました。 この素数は各計算のモジュラスとしても使用されるため、結果として得られる共有秘密の鍵空間全体は0-12にしかなりません。 この数が大きいほど、攻撃者が共有秘密を強制的に強制する時間が長くなります。

明らかに、数学を比較的単純に保つために、上記の非常に小さな数字を使用していました。 真のDH交換は、非常に大きい数字で数学をやっています。 Diffie-Hellmanの数字には3つの典型的なサイズがあります:

ビットサイズは素数への参照です。 これは、結果として得られる共有秘密の鍵空間全体に直接相当します。 このキースペースがどれだけ大きいかを知るには、

768ビットの数値を完全に書き出すには、232桁の10進数が必要です。
1024ビットの数値を完全に書き出すには、309桁の10進数が必要です。
1536ビットの数値を完全に書き出すには、463桁の10進数が必要です。

共有秘密の使用

共有秘密が達成されると、一般的には、共同対称暗号化鍵および/または共同HMAC鍵（セッション鍵とも呼ばれる）を確立するために計算

しかし、共有秘密自体を秘密鍵として直接使用すべきではないことを指摘することは重要です。 もしそうであれば、あなたが保証できるのは、安全な会話を通して、あなたはまだDiffie-Hellman交換の反対側にあった同じ当事者に話しているということです。

しかし、あなたはまだ相手が誰であるかについての確認や保証を持っていません。 ただ、誰もあなたの安全な会話の途中で突然彼らのふりをすることはできません。

実際のセッション鍵の生成には、DH共有秘密鍵と、選択した認証スキームのように、意図した相手にのみ知られている他の値を含める必要があります。

テキストよりもビデオコンテンツを好む？ この記事の大部分は記録されており、Youtubeで見ることができます:

シリーズナビ>>