디피-헬만

어떻게 붐비는 방에 두 사람이 듣고 될 수있는 다른 사람에게 비밀을 공개하지 않고,단지 쌍이 알고있는 비밀을 도출 할 수 있습니까?

이것이 바로 디피-헬만 키 교환이 해결해야 할 시나리오이다.

디피헬만 키 교환은 두 당사자가 서로에 대한 사전 지식이 없어도 비보안 채널을 통해 공유된 비밀을 공동으로 확립하는 수단이다.

그들은 실제로 비밀을 교환하지 않으며,둘 다 결합하여 동일한 결과 값을 얻을 수있는 일부 값만 교환합니다.

개념적으로,디피-헬만 키 교환을 시각화하는 가장 좋은 방법은 유비쿼터스 페인트 색상 혼합 데모입니다. 당신이 그것에 익숙하지 않다면 그것을 빨리 검토 할 가치가 있습니다.

그러나,이 문서에서 우리는 한 단계 더 가서 실제로 당신에게 디피-헬만 키 교환의 수학을 보여주고 싶습니다.

디피 헬만의 수학에 들어가기 전에 소수가 무엇인지,모듈러스 연산이 무엇인지(일명 나머지 나누기)에 대한 기본적인 이해를 원할 것입니다. 이 두 용어는 다른 기사에서 정의되었습니다.

아래는 앨리스와 밥 사이의 디피-헬만 교환의 모든 단계를 요약 한 인포 그래픽입니다.

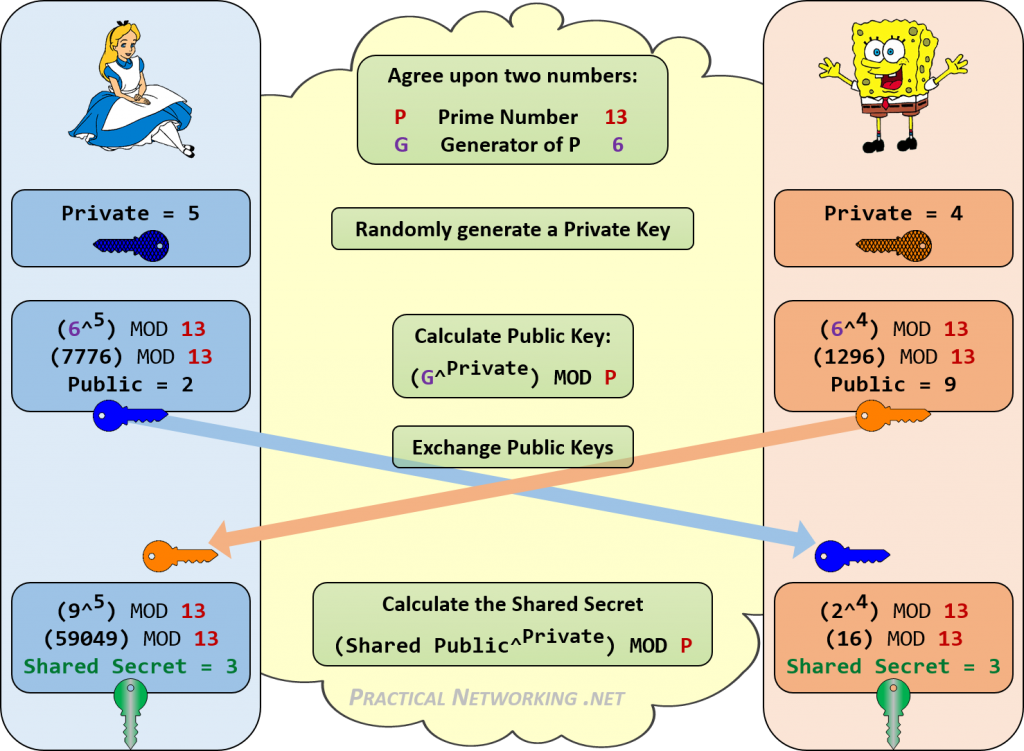
앨리스와 밥이 어떻게 3 의 동일한 공유 비밀을 달성 할 수 있었는지 주목하십시오. 키 교환을 듣는 사람은 누구나 공개 값과 시작 피 및 지 값 만 알 수 있습니다. 3 을 달성하기 위해 그 숫자(13,6,2,9)를 결합하는 일관된 방법이 없습니다.

이 예에서는 13 의 소수를 사용했습니다. 이 소수는 또한 각 계산에 대한 계수로 사용되기 때문에 결과 공유 비밀에 대한 전체 키 공간은 0-12 만 될 수 있습니다. 이 숫자가 클수록 공격자가 공유 된 비밀을 무차별 적으로 강요하는 시간이 더 어려워집니다.

분명히 우리는 수학을 비교적 간단하게 유지하기 위해 위의 매우 작은 숫자를 사용하고있었습니다. 진정한 디엠 교환은 훨씬 더 큰 숫자에 수학을하고 있습니다. 디피-헬만의 숫자에 세 가지 일반적인 크기가 있습니다:

비트 크기는 소수에 대한 참조입니다. 이는 결과 공유 암호의 전체 키 공간과 직접 동일합니다. 이 키 공간이 얼마나 큰지에 대한 아이디어를 얻으려면

768 비트 숫자를 완전히 작성하려면 232 개의 10 진수가 필요합니다.
1024 비트 숫자를 완전히 쓰려면 309 개의 10 진수가 필요합니다.
1536 비트 숫자를 완전히 작성하려면 463 개의 10 진수가 필요합니다.

공유 비밀 사용

공유 비밀이 달성되면 공동 대칭 암호화 키 및/또는 공동 암호화 키(세션 키라고도 함)를 설정하는 계산에 일반적으로 사용됩니다.

그러나 공유 비밀 자체가 비밀 키로 직접 사용되어서는 안된다는 점을 지적하는 것이 중요합니다. 만약 그렇다면,당신이 확신 할 수있는 것은 안전한 대화를 통해 당신은 여전히 디피-헬만 교환의 반대편에 있던 동일한 당사자에게 말하고 있다는 것입니다.

그러나 상대방이 누구인지에 대한 확인이나 보증은 아직 없습니다. 다만 다른 사람이 갑자기 당신의 안전한 대화의 한가운데에 그(것)들인 것을 가장할 수 있다 다만.

실제 세션 키의 생성에는 사용자가 선택한 인증 체계와 같이 의도된 상대방에게만 알려진 다른 값과 함께 공유 암호가 포함되어야 합니다.

텍스트보다 비디오 콘텐츠를 선호하십니까? 이 문서의 대부분은 기록 된 유튜브에서 볼 수 있습니다:

시리즈 탐색 예제>>