

0
0

0
내가 여러 번 언급 한 바와 같이,수학 교육의 주요 목표 중 하나는 자신감 문제 해법을 마련하는 것입니다. 그리고 수학 문제를 해결하는 데는 여러 가지 방법이 있지만 어른으로서 우리는 종종 전략을 상식으로 볼 수 있습니다. 당신이”풀어”그들의 창조적 인 마음이 작동하고 탐구 볼 수 있도록 가능한 한 많은 도구를 제공하는 것은 성공을 위해 그들을 설정합니다. 문제를 가르치는 아이에 나의 시리즈를 계속하기 위하여는,오늘 나는 명부를 만들어서 문제 해결을 토론하기 위하여 가고 있다 해결한다.

–>잠깐만! 당신의 아이의 감각을 만들고 단어 문제를 해결하는 데 도움이 필요하십니까? 이 편집 가능한 단어 문제 해결 템플릿 세트를 좋아할 것입니다! 모든 유형의 단어 문제에 대해 모든 학년과 함께 사용하십시오:
의미있는 목록 만들기:
이것은 수학처럼 보이지 않으며 종종 시간이 많이 걸릴 수 있기 때문에 개인적으로 항상 어려운 접근 방식이었습니다. 내 말은,누가 정말로 앉아서 수학 문제에 대한 가능한 모든 해결책을 나열하고 싶습니까? 그러나,아주 유용한 전략 이고,우리가 보기 때문에,편성되는 것을 배우 체계 열쇠 이다(또한 시간의 톤을 저장할 것이다)!
그렇다면 목록을 만드는 것이 언제 유용합니까? 기본적으로 둘 이상의 솔루션이 있는 문제가 있거나 조합 문제를 해결하려고 할 때마다 목록을 만드는 것이 도움이 됩니다.
그러나 단지 가능성의 목록이 아닙니다. 당신은 단지 어디에서 가능성을 꺼내려고하는 경우 그 쓸모과 좌절 느낄 것이다. 그리고 그 이상,그것은 가능성이 매우 가능성이 건너 뛰거나 반복 될 것입니다,최종 솔루션을 잘못 만들기.
그 외에도 체계적인 접근 방식이 없다면 목록을 만드는 데 더 많은 시간이 소요될 것입니다. 아무도는 다만 앉고 싶고 그들의 두뇌로 해결책을 희망하는 종이에 응시 터질 것이다.
정보를 논리적인 방식으로 구성하면 추적할 수 있고 가능한 모든 해결 방법을 찾을 수 있습니다.
정보를 구성하는 방법에는 여러 가지가 있지만,그 아이디어는 계속 진행하기 전에 목록의 한 부분으로 모든 가능성을 소진하는 것입니다.
예를 들어,지역 아이스크림 가게에서 아이스크림 토핑의 모든 다른 조합을 알아 내려고한다고 가정 해보십시오. 그들은 3 가지 맛(초콜릿,바닐라 및 딸기)을 가지고 있지만 4 가지 토핑(견과류,휘핑 크림,초콜릿 사탕 및 거미 곰)도 있습니다.
어떤 종류의 구조도 없이 다른 가능성을 나열하기 시작하면 목록에서 길을 잃고 무언가를 놓칠 수밖에 없다. 이렇게 대신,위에 바닐라로 이동하기의 앞에 초콜렛 아이스크림을 위해 모든 가능성을 목록으로 만들십시요.
초콜릿:초콜릿(토핑 없음),견과류가 든 초콜릿,휘핑 크림이 든 초콜릿,사탕이 든 초콜릿,젤리 곰이 든 초콜릿.
이제 우리는 당신이 초콜릿 아이스크림을 얻을 경우 5 가능성이 있다는 것을 볼,그래서 우리는 바닐라,다음 딸기로 이동할 수 있습니다.
핵심은 첫 번째 맛부터 시작하여 가능한 모든 토핑을 순서대로 나열하는 것입니다. 그런 다음 맛으로 이동하고 같은 순서로 토핑을 통해 이동합니다.
그러면 아무 것도 건너 뛰거나 잊어 버리거나 반복되지 않습니다. 목록을 완료 한 후 15 가지 가능한 조합이 있음을 알 수 있습니다.
일부 학생들은 각 맛에 대해 5 가지 가능성이 있음을 알 수 있으므로 목록을 작성하지 않고 3 가지 5 가지를 곱할 수 있습니다. (그것은 또 다른 훌륭한 전략입니다:패턴을 찾으십시오).
패턴이 발견되지 않더라도,체계적이고 체계적인 방식으로 목록을 완성하면 모든 가능성이 커버되고 전체(15)가 발견된다.
목록을 구성하는 또 다른 방법은 트리 다이어그램을 만드는 것입니다. 또 다른 예제 문제가 있습니다:
사라는 휴가 중이며 3 쌍의 바지(파란색,검은 색 및 흰색)와 3 개의 셔츠(분홍색,노란색 및 녹색)를 가져 왔습니다. 그녀는 얼마나 많은 다른 의상 조합을 만들 수 있습니까?
트리 다이어그램을 사용하면 특히 목록을 추적하는 데 어려움을 겪는 어린이가있는 경우 정보를 정리할 수있는 좋은 방법입니다:
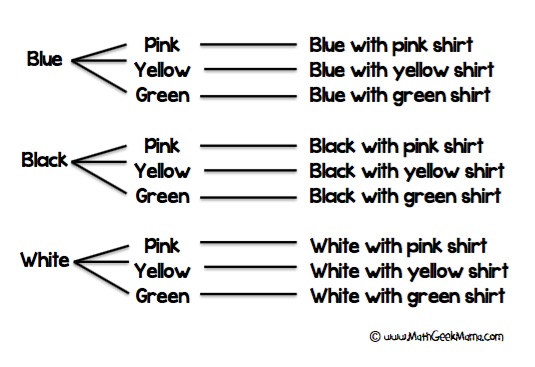
그런 다음 학생들은 9 가지 의상 조합이 있다는 것을 쉽게 알 수 있습니다.

도움이 되었나요? 그것은 당신이 당신의 아이들과 함께 공유하는 전략인가?
이 시리즈의 나머지 게시물을보고 아이들이 큰 문제 해결사가 될 수 있도록 준비하십시오.:
- 보다 쉬운 문제 해결
- 그림을 그려 문제 해결
- 거꾸로 작업하여 문제 해결
- 패턴을 찾아 문제 해결
- 추측으로 문제 해결&확인