법 수학 공식

학생들이 알아야 할 법 수학 공식과 암기 팁?

법 수학 섹션은 학생들이 60 분 이내에 응답해야 60 다섯 다중 선택 질문을 포함한다. 질문은 11 학년까지 덮여 여섯 주제 영역에서 그려집니다. 여기에는 사전 대수학,중급 대수학,초등 대수학,좌표 기하학,삼각법 및 평면 기하학이 포함됩니다.

다음은 수학 법 시험에서 다루는 주제와 기술이다.

대수

섹션은 14 질문을 포함하고 소수,정수,분수,비율,양의 정수 힘,정수,제곱근,백분율 및 비율에 학생을 테스트합니다. 테스트 다른 주제는 하나의 변수,선형 방정식,절대 값,배수 및 요인,중앙값,평균,모드,데이터 해석 및 계산 문제와 확률을 포함한다.

중급 대수

이 부분은 불평등,절대 값,이차 공식,방정식의 시스템,합리적이고 급진적 인 표현,함수,이차 부등식,다항식,행렬,복소수의 학생을 테스트 아홉 질문을 포함한다.

초등 대수

다항식,변수,인수 분해,정수 지수,제곱근,선형 부등식 및 2 차 방정식을 만지는 영역에서 약 10 개의 질문이있을 것입니다.

평면 기하학

사각형,평행 사변형,삼각형,사다리꼴 및 원과 같은 평면 그림을 터치하는 14 개의 질문이 있습니다. 일부 질문은 수직선,회전,3 차원 기하학,면적,둘레,논리적 추론,부피,번역 및 반사에 대한 지식을 테스트합니다.

좌표 기하학

포인트,숫자 선 그래프,원,다항식,선,곡선,중간 점 공식,원뿔,변환,거리 공식,방정식 및 그래프 관계,기울기 및 수직 및 평행선의 속성에 대한 영역 테스트에서 약 9 개의 질문이 있습니다.

섹션에서 삼각법은 삼각 함수,방정식 및 정체성,직각 삼각형 삼각 비율 및 삼각 함수 모델링에 대한 네 가지 질문을 찾을 수 있습니다.

법 수학 공식 목록

다음은 법 시험을 위해 알아야 할 13 법 수학 공식의 목록입니다:

1. 산술 평균
2. 확률
3. 2 차 방정식
4. 거리 공식
5. 기울기 공식
6. 기울기 절편 공식
7. 중간점 공식
8. 삼각형의 면적
9. 피타고라스의 정리
10. 사각형과 둘레의 면적
11. 입방체의 부피
12. 원의 면적
13. 삼각 공식

산술 평균

이것은 평균과 동일하며,이것은 평균의 합이다.모든 항목을 항목 수로 나눈 값입니다. 예를 들어 값의 평균을 계산하면 합계를 값 수로 나눈 값

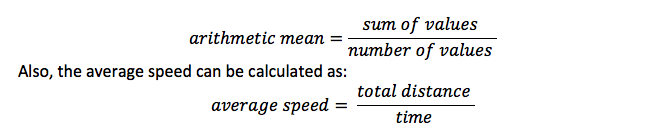
확률 공식

확률은 가능한 결과 집합에서 어떤 일이 발생할 횟수의 가능성을 계산하는 데 사용됩니다. 그것은 어떤 일이 일어날 가능성을 나타내는 것입니다. 1 의 확률은 일어날 특정 무언가가 있다는 것을 의미하지만 0 의 가능성은 일어나지 않을 것을 의미합니다.

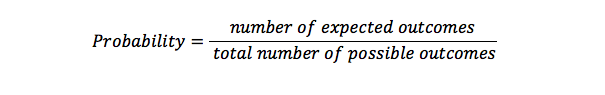
2 차 방정식

다음과 같이 표현 된 공식:2 차 방정식(1 차 방정식)은 2 차 방정식(1 차 방정식)과 2 차 방정식(1 차 방정식)의 합입니다.

거리 공식

수식은 좌표 평면에서 두 점 사이의 거리를 계산할 때 사용됩니다. 이 공식은 다음과 같이 표현된다:

디=1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000예를 들어,점이있는 경우(엑스 1,와이 1)및 비(엑스 2,와이 2),기울기를 다음과 같이 계산할 수 있습니다.:

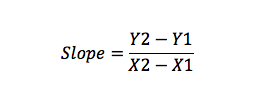
기울기 절편 공식

기울기 절편 공식은 다음과 같이 표현 된 선 방정식입니다.:

• 미디엄 선의 기울기를 나타내는 반면 비 이다 와이-절편 여기서 와이-절편 점이 와이 축을 교차합니다.
• 선이 원점을 통과 할 경우 와이-절편은 0 이고 방정식은 다음과 같이 표현됩니다.

중간점 공식

선의 중간점을 찾는 공식입니다. 예를 들어 두 점이있는 경우 ㅏ(엑스 1,와이 1)및 비(엑스 2,와이 2),중간 점은 다음과 같습니다:

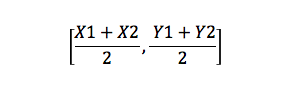
삼각형의 면적

삼각형으로 묶인 전체 면적을 계산하기 위해 다음과 같이 표현된 수식을 사용합니다.

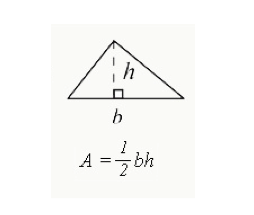
• 이 경우 삼각형의 높이를 계산해야합니다. 직각 삼각형의 높이는 90 도 각도의 변이 됩니다. 위의 그림과 같이 다른 삼각형의 경우 높이가 삼각형의 내부 아래로 떨어집니다.

피타고라스 정리

피타고라스 정리는 두 변이 알려진 직각 삼각형의 알 수없는 측면을 계산할 때 중요합니다. 수식은 다음과 같이 표현됩니다. 두 개의 짧은 변의 합은 긴 변의 합과 같습니다.

사각형과 둘레의 지역

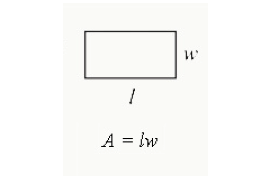
사각형의 영역을 찾으려면 길이에 너비를 곱합니다. 사각형안에 둘러싸는 총계 지역 이다.반면에 사각형의 둘레는 그 주위의 거리이다.이 경우 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의 삼각형의 두 개의

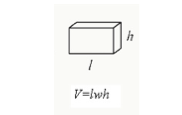
직육면체의 길이,너비 및 높이를 곱하여 직육면체의 부피를 계산할 수 있습니다.

원의 면적

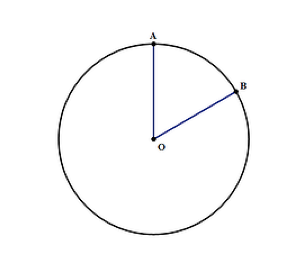
원의 면적은 공식을 사용하여 찾을 수 있습니다.:

• 3 은 3 으로 작성된 상수입니다.당신이 시험하는 동안 계산기가없는 경우 기억하는 것이 중요하다(14)
• 아르 자형-위의 그림과 같이 원의 반경이다. 즉,원주 주위의 거리를 원주 둘레로 지칭한다. 이 경우 원의 둘레는 다음과 같이 계산됩니다.:
  • 디,이 직경은 원의 반지름의 두 배입니다. 이 원의 두 끝을 만지고 두 반으로 원을 분할 선입니다.

  삼각 수식 사인(소),코사인(카),탄젠트(토아))

  

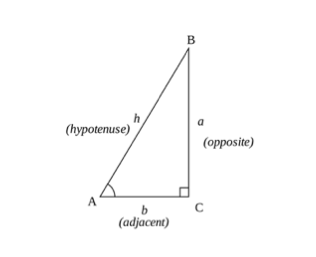
  삼각 계산은 사인,코사인 및 탄젠트 규칙을 사용하여 삼각형의 기본 개념으로 요약 할 수 있습니다. 삼각형의 변을 사용하여 각도의 코사인,사인 또는 탄젠트를 계산할 수 있습니다.

  

  어디:

  • 반대쪽 변-각도와 반대되는 삼각형의 변()
  • 인접한 변-가장 긴 변이 아닌 각도에 가장 가까운 변입니다.
  • 빗변은 삼각형의 가장 긴 변입니다.

  법 수학 공식 및 방정식 암기 팁

  법 시험 중 수식을 암기하려면 수학 시험에 지정된 주제 영역을 읽음으로써 일찍 익숙해지는 것이 중요합니다.

  당신은 또한 공식을 마스터하기 위해 가능한 한 많은 문제를 시도하여 연습 할 수 있습니다.

  수식을 더 크게 말하거나 차트에 쓰고 방에 붙이는 것과 같은 다른 채널을 사용하면 수식을 기억하는 데 도움이 될 수 있습니다.