Hvilke ACT Math Formler Bør Elevene Vite Og Tips For Å Huske dem?
ACT Math-delen består av 60 fem-flervalgsspørsmål som studentene skal svare på innen 60 minutter. Spørsmålene er hentet fra seks emneområder dekket opp til 11. klasse. De inkluderer Pre-algebra, mellomliggende algebra, elementær algebra, koordinatgeometri, trigonometri og plangeometri.
Her er emnene og ferdighetene som dekkes Av Math ACT-testen.
Algebra
seksjonen består av 14 spørsmål Og tester studenten på desimaler, hele tall, brøker, forhold, positive heltallskrefter, heltall, kvadratrøtter, prosent og andel. Andre emner som testes inkluderer en variabel, lineære ligninger, absoluttverdi, multipler og faktorer, median, middel, modus, datatolking og telleproblemer og sannsynlighet.
Intermediate Algebra
denne delen består av ni spørsmål som tester studenten i ulikheter, absoluttverdi, kvadratisk formel, likningssystemer, rasjonelle og radikale uttrykk, funksjoner, kvadratiske ulikheter, polynomer, matriser og komplekse tall.
Elementær Algebra
det vil være rundt ti spørsmål i området som berører polynomer, variabler, factoring, heltall eksponenter, kvadratrøtter, lineære ulikheter og kvadratiske ligninger.
Plane Geometry
du vil ha 14 spørsmål berøre på flyet tall som rektangler, parallellogrammer, trekanter, trapeser, og sirkler. Noen spørsmål teste kunnskap på vinkelrette linjer, rotasjoner, 3-D geometri, areal, omkrets, logisk resonnement, volum, oversettelser og refleksjoner.
Koordinere Geometri
det vil rundt ni spørsmål fra området testing på grafen av poeng, antall linje grafer, sirkler, polynomer, linjer, kurver, midtpunkt formel, kjeglesnitt, transformasjoner, avstand formel, ligninger, og graf relasjoner, skråning, og egenskaper av vinkelrette og parallelle linjer.
I Seksjonen Vil Trigonometri finne fire spørsmål om trigonometriske funksjoner, ligninger og identiteter, høyre trekant trigonometriske forhold og trigonometriske funksjoner modellering.
Liste OVER ACT Math Formler
her er en liste over 13 ACT math formler du trenger å vite FOR ACT test:
- Aritmetisk Gjennomsnitt
- Sannsynlighet
- Kvadratisk Ligning
- Avstandsformel
- Skråningsformel
- Midtpunktsformel
- Område Av En Trekant
- pythagoras ‘ læresetning
- Område Av Rektangel Og Omkrets
- Volum Av Kuboid
- Område Av En Sirkel
- Trigonometriske Formler
Aritmetisk Gjennomsnitt
Dette Er Det Samme Som Gjennomsnitt, Og Det Er Summen av alle elementer dividert med antall elementer. Hvis du for eksempel beregner gjennomsnittet av verdier, delte du summen med antall verdier
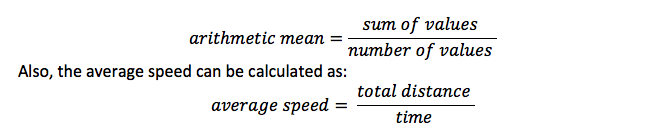
Sannsynlighetsformel
Sannsynlighet brukes til å beregne muligheten for antall ganger noe vil skje i et sett med mulige resultater. Det er en representasjon av sjansene for at noe skjer. En sannsynlighet på 1 betyr at det er et bestemt noe som vil skje, men en mulighet for 0 betyr at noe ikke vil skje.
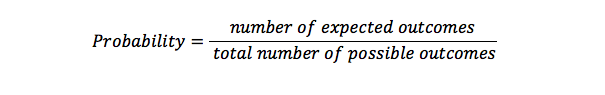
Kvadratisk Ligning
formelen uttrykt som:
x = – b ± √ b2-4ac / 2a
det brukes til å bestemme x-avskjær av en parabolisk eller kvadratisk ligning.
Avstandsformel
formelen brukes ved beregning av avstanden mellom to punkter på et koordinatplan. Formelen er uttrykt som:
d=√(x ^ – x₂)2 + (y ^ – y₂)2
Hellingsformel
hellingen er et mål på linjeendringer uttrykt som y-akseendringen divideres med endringen På X-aksen (stigning/løp).
for eksempel, hvis du har punkt A (X1, Y1) Og B (X2, Y2), kan du beregne helling som:
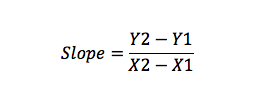
Slope Intercept Formula
slope-intercept-formelen er en linjeligning uttrykt SOM Y=MX + b der:
- M står For linjens skråning, mens b er y-skjæringspunktet der y-skjæringspunktet krysser y-aksen.
- hvis linjen vil passere gjennom opprinnelsen, er y-avskjæringen null, og ligningen vil bli uttrykt SOM Y=MX.
Midtpunktsformel
dette er en formel som finner midtpunktet til en linje. For eksempel, hvis du har to punkter, A(X1, Y1) Og B (X2, Y2), så vil midtpunktet være:
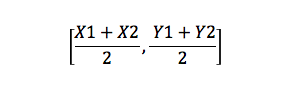
Arealet Av En Trekant
formelen uttrykt som ½ (base x høyde) brukes til å beregne det totale arealet innelukket i en trekant.
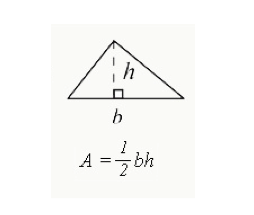
- b= bunnen av trekanten (kanten på den ene siden)
- h=høyden på en trekant. Høyden for en rettvinklet trekant vil være siden med en 90 graders vinkel. For andre trekanter vil høyden falle ned i det indre av trekanten,som vist ovenfor.
Pythagoras ‘Læresetning
Pythagoras’ læresetning er avgjørende for å beregne en rettvinklet trekants ukjente side når to sider er kjent. Formelen er uttrykt som a2 + b2=c2. Summen av to kortere sider er lik summen av den lengre siden.

Areal Av Rektangel Og Perimeter
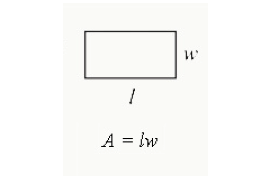
hvis du vil finne et rektangelområde, multipliserer du lengden med bredden. Det er det totale arealet som er innelukket i et rektangel.
Område = Lengde x Bredde
på den annen side er et rektangeles omkrets avstanden rundt den.
Perimeter = (L+B+L+W) forenklet som 2 (L + W)
Volum Av Kuboid
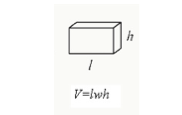
du kan beregne en cuboid volum ved å multiplisere lengde, bredde og høyde på cuboid.
Område Av En Sirkel
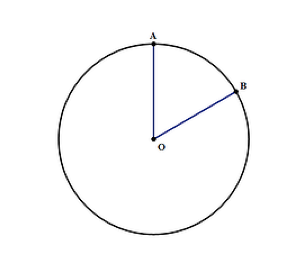
en sirkels område kan bli funnet ved hjelp av formelen nr2 hvor:
- π er en konstant som er skrevet som 3.14, som er viktig å huske om du ikke vil ha en kalkulator under testen
- r-er sirkelens radius, som i diagrammet ovenfor. Det er avstanden Fra o til kanten av sirkelen ved punkt a eller B
tilsvarende er avstanden rundt sirkelen referert til som omkretsen. Det beregnes som:
Omkrets av sirkelen = nd eller 2nr
Hvor:
- D, som er diameteren er to ganger sirkelens radius. Det er linjen som deler sirkelen i to halve berører to ender av en sirkel.
Trigonometriske Formler Sinus (SOH), Cosinus (CAH), Tangent (TOA)
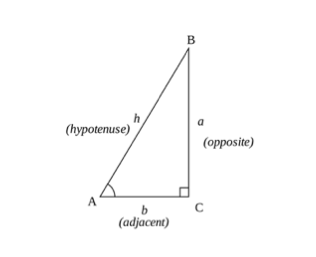
Trigonometriske beregninger kan oppsummeres av grunnleggende begreper i en trekant ved hjelp av sinus, cosinus, og tangent regler (SOHCAHTOA). Du kan beregne cosinus, sinus, eller tangent av en vinkel ved hjelp av en trekant sider.

Hvor:
- Motsatt side-er trekantens side som er motsatt vinkelen ()
- Tilstøtende side-er siden som er nærmest vinkelen, men ikke den lengste siden.
- hypotenusen er trekantens lengste side.
Tips For Å Huske ACT Matematiske Formler Og Ligninger
for å huske formlene under ACT-eksamenen, er det viktig å gjøre deg kjent tidlig ved å lese i emneområdene som er angitt for Matteprøven.
du kan også øve ved å prøve så mange problemer som mulig for å mestre formelen.
Bruk av forskjellige kanaler som å si formlene høyere eller skrive dem på diagrammer og stikke dem i rommet ditt, kan hjelpe deg med å huske formlene.