Diffie-Hellman

Hvordan kan to personer i et overfylt rom utlede en hemmelighet som bare paret vet, uten å avsløre hemmeligheten til noen andre som kan lytte?

det er akkurat scenariet Diffie-Hellman Nøkkelutveksling eksisterer for å løse.

Diffie-Hellman-Nøkkelutvekslingen er et middel for to parter til i fellesskap å etablere en felles hemmelighet over en usikker kanal uten å ha noen forkunnskaper om hverandre.

de utveksler aldri hemmeligheten, bare noen verdier som begge kombinerer som lar dem oppnå samme resulterende verdi.

Konseptuelt er Den Beste måten å visualisere Diffie-Hellman-Nøkkelutvekslingen med den allestedsnærværende fargeblandingsdemonstrasjonen. Det er verdt å raskt vurdere det hvis du ikke er kjent med det.

men i denne artikkelen vil vi gå et skritt videre og faktisk vise deg matematikken I Diffie-Hellman-Nøkkelutvekslingen.

DH Math

Før Du kommer inn i matematikken Til Diffie-Hellman, vil du ha en grunnleggende forståelse av hva Et Primtall er, og hva Moduloperasjonen er(aka, rest divisjon). Begge disse begrepene er definert i en annen artikkel.

Nedenfor er en infografisk som beskriver alle trinnene I Diffie-Hellman-utvekslingen Mellom Alice og Bob.

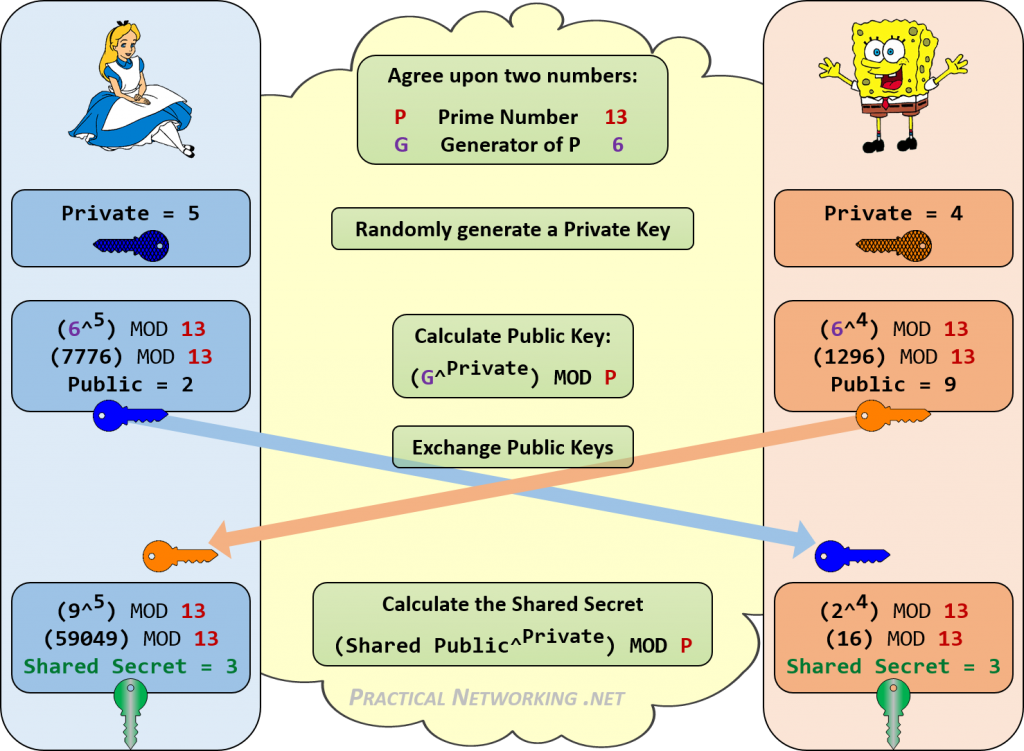
Legg merke til hvordan Både Alice og Bob var i stand til å oppnå Samme Delte Hemmelighet av 3. Alle som lytter inn på DERES Dh-Nøkkelutveksling, vil bare kjenne De Offentlige Verdiene, og start P – og G-verdiene. Det er ingen konsekvent måte å kombinere disse tallene (13, 6, 2, 9) for å oppnå 3.

DH-Tall

i vårt eksempel brukte Vi Et Primtall på 13. Siden Dette Primtallet også brukes som Modul For hver beregning, kan hele nøkkelplassen for den resulterende Delte Hemmeligheten bare være 0-12. Jo større dette tallet, desto vanskeligere vil en angriper ha i brute tvinge din delte hemmelighet.

Åpenbart brukte vi svært små tall over for å holde matematikken relativt enkel. Sanne dh-utvekslinger gjør matte på tall som er langt større. Det er tre typiske størrelser til tallene I Diffie-Hellman:

bitstørrelsen er en referanse til Primtallet. Dette tilsvarer direkte hele nøkkelrommet til den resulterende Delte Hemmeligheten. For å gi deg en ide om hvor stor denne nøkkelplassen er:

for å kunne skrive ut et 768 bitnummer, trenger du 232 desimaler.
for å kunne skrive ut et 1024 bitnummer, trenger du 309 desimaler.
for å kunne skrive ut et 1536 bitnummer, trenger du 463 desimaler.

Ved Hjelp Av Den Delte Hemmeligheten

når Den Delte Hemmeligheten er oppnådd, blir den vanligvis brukt i beregningen for å etablere en Felles Symmetrisk Krypteringsnøkkel og / Eller EN FELLES HMAC-Nøkkel – også kjent som Øktnøkler.

men Det er viktig å påpeke At Den Delte Hemmeligheten i seg selv ikke skal brukes direkte som Hemmelig Nøkkel. Hvis det var, alt du kan være trygg på er at hele sikker samtale du fortsatt snakker til samme parti som var På den andre siden Av Diffie-Hellman utveksling.

du har imidlertid fortsatt ingen bekreftelse eller forsikring om hvem den andre parten er. Bare at ingen andre kan plutselig later til å være dem i midten av sikker samtale.

genereringen av De faktiske Øktnøklene bør inkludere Dh-Delt Hemmelighet, sammen med en annen verdi som bare ville være kjent for den tiltenkte andre parten, som noe fra Godkjenningsskjemaet du valgte.

Foretrekker du videoinnhold fremfor tekst? Flertallet av denne artikkelen har blitt registrert og kan ses På Youtube:

Serie Navigasjon Rsa Eksempel > >