Diffie-Hellman

jak dwoje ludzi w zatłoczonym pokoju może odkryć sekret, który zna tylko para, nie ujawniając go nikomu innemu, kto mógłby go słuchać?

dokładnie taki scenariusz istnieje do rozwiązania Wymiana kluczy Diffiego-Hellmana.

Wymiana kluczy Diffiego-Hellmana jest środkiem dla dwóch stron do wspólnego ustanowienia wspólnej tajemnicy na niezabezpieczonym kanale, bez uprzedniej wiedzy o sobie.

w rzeczywistości nigdy nie wymieniają tajemnicy, tylko niektóre wartości, które łączą się, co pozwala im osiągnąć tę samą wartość wynikową.

koncepcyjnie najlepszym sposobem na wizualizację wymiany kluczy Diffie-Hellman jest wszechobecna demonstracja mieszania kolorów farb. Warto go szybko przejrzeć, jeśli nie jesteś z nim zaznajomiony.

jednak w tym artykule chcemy pójść o krok dalej i faktycznie pokazać ci matematykę w wymianie kluczy Diffiego-Hellmana.

Dh Math

zanim przejdziesz do matematyki Diffiego-Hellmana, będziesz chciał mieć podstawowe zrozumienie, czym jest liczba pierwsza i czym jest operacja modułowa (inaczej dzielenie reszty). Oba te terminy zostały zdefiniowane w innym artykule.

poniżej znajduje się infografika przedstawiająca wszystkie etapy wymiany Diffie-Hellman pomiędzy Alice i Bobem.

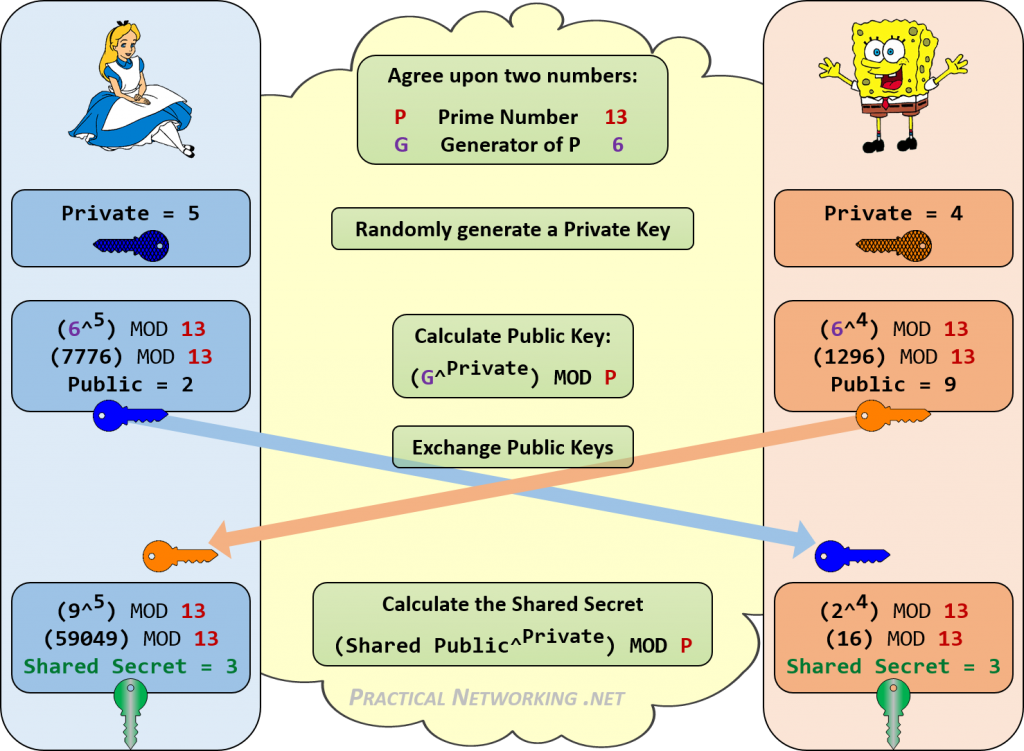
zauważ, jak zarówno Alice, jak i Bob byli w stanie osiągnąć ten sam wspólny sekret 3. Każdy, kto słucha wymiany kluczy DH, zna tylko wartości publiczne oraz początkowe wartości P i G. Nie ma spójnego sposobu łączenia tych liczb (13, 6, 2, 9), aby uzyskać 3.

liczby DH

w naszym przykładzie użyliśmy liczby pierwszej 13. Ponieważ ta liczba pierwsza jest również używana jako moduł dla każdego obliczenia, cała przestrzeń klucza dla wynikowego wspólnego sekretu może wynosić tylko 0-12. Im większa liczba, tym trudniej będzie atakującemu w brutalnym wymuszaniu Twojej wspólnej tajemnicy.

oczywiście używaliśmy bardzo małych liczb powyżej, aby pomóc utrzymać matematykę stosunkowo prostą. Prawdziwe wymiany DH robią matematykę na liczbach, które są znacznie większe. Istnieją trzy typowe rozmiary liczb w Diffie-Hellman:

rozmiar bitu jest odniesieniem do liczby pierwszej. Odpowiada to bezpośrednio całej przestrzeni kluczowej powstałej wspólnej tajemnicy. Aby dać ci wyobrażenie o tym, jak duża jest ta przestrzeń klucza:

aby w pełni zapisać liczbę 768 bitów, potrzebujesz 232 cyfr dziesiętnych.
aby w pełni zapisać 1024-bitową liczbę, potrzebujesz 309 cyfr dziesiętnych.
aby w pełni zapisać liczbę 1536 bitów, potrzebujesz 463 cyfr dziesiętnych.

korzystanie ze współdzielonego klucza

po osiągnięciu współdzielonego klucza zwykle jest używane w obliczeniach do ustanowienia wspólnego symetrycznego klucza szyfrowania i/lub wspólnego klucza HMAC – znanego również jako klucze sesji.

ale ważne jest, aby podkreślić, że sam udostępniony sekret nie powinien być bezpośrednio używany jako klucz tajny. Gdyby tak było, możesz mieć pewność, że podczas bezpiecznej rozmowy nadal rozmawiasz z tą samą stroną, która była po drugiej stronie wymiany Diffie-Hellman.

jednak nadal nie masz potwierdzenia ani pewności co do tego, kim jest druga strona. Tylko, że nikt inny nie może nagle udawać, że jest nimi w trakcie bezpiecznej rozmowy.

generowanie rzeczywistych kluczy sesji powinno zawierać udostępniony sekret DH wraz z inną wartością, która byłaby znana tylko zamierzonej drugiej Stronie, na przykład z wybranego schematu uwierzytelniania.

wolisz treści wideo od tekstu? Większość tego artykułu została nagrana i można ją obejrzeć na Youtube:

Seria Nawigacja RSA przykład > >