formuły matematyczne ACT

jakie formuły matematyczne ACT powinni znać uczniowie i wskazówki, aby je zapamiętać?

dział matematyki ACT składa się z 60 pytań wielokrotnego wyboru, na które uczniowie powinni odpowiedzieć w ciągu 60 minut. Pytania pochodzą z sześciu obszarów tematycznych objętych do 11 klasy. Obejmują one algebrę wstępną, algebrę pośrednią, algebrę elementarną, geometrię współrzędnych, trygonometrię i geometrię płaszczyzny.

oto tematy i umiejętności zawarte w teście z matematyki.

Algebra

sekcja zawiera 14 pytań i testów ucznia na ułamki dziesiętne, liczby całkowite, ułamki, stosunek, dodatnie moce całkowite, liczby całkowite, pierwiastki kwadratowe, procent i proporcja. Inne badane tematy obejmują jedną zmienną, równania liniowe, wartość bezwzględną, wielokrotności i czynniki, medianę, średnią, tryb, interpretację danych oraz problemy z liczeniem i prawdopodobieństwem.

Algebra pośrednia

ta część zawiera dziewięć pytań testujących ucznia w zakresie nierówności, wartości bezwzględnej, formuły kwadratowej, systemów równań, wyrażeń racjonalnych i radykalnych, funkcji, nierówności kwadratowych, wielomianów, macierzy i liczb zespolonych.

Algebra elementarna

będzie około dziesięciu pytań dotyczących wielomianów, zmiennych, faktoringu, wykładników liczb całkowitych, pierwiastków kwadratowych, nierówności liniowych i równań kwadratowych.

Geometria płaszczyzny

będziesz miał 14 pytań dotykających figur płaskich, takich jak prostokąty, równoległobok, trójkąty, trapezy i okręgi. Niektóre pytania sprawdzają wiedzę na temat linii prostopadłych, obrotów, geometrii 3D, powierzchni, obwodu, logicznego rozumowania, objętości, tłumaczeń i odbić.

Geometria współrzędnych

będzie około dziewięciu pytań z obszaru testowania na wykresie punktów, Wykresów linii liczbowych, okręgów, wielomianów, linii, krzywych, wzoru punktu środkowego, stożków, przekształceń, wzoru odległości, równań i relacji Wykresów, nachylenia i właściwości prostopadłych i równoległych linii.

w sekcji Trygonometria znajdziesz cztery pytania dotyczące funkcji trygonometrycznych, równań i tożsamości, współczynników trygonometrycznych trójkąta prostokątnego i modelowania funkcji trygonometrycznych.

lista formuł matematycznych ACT

Oto lista 13 formuł matematycznych ACT, które musisz znać do testu ACT:

1. średnia arytmetyczna
2. prawdopodobieństwo
3. Równanie kwadratowe
4. wzór odległości
5. wzór nachylenia
6. punkt środkowy
7. obszar trójkąta
8. twierdzenie Pitagorasa
9. pole prostokąta i obwód
10. objętość prostopadłościanu
11. pole Okręgu
12. wzory trygonometryczne

średnia arytmetyczna

to jest to samo co średnia i jest to suma wszystkich elementów podzielonych przez liczbę elementów. Na przykład, obliczając średnią wartości, podzieliłeś sumę przez liczbę wartości

act-exam-średnia arytmetyczna-formula_8874>

prawdopodobieństwo Formula_8071>

Prawdopodobieństwo jest używane do obliczania możliwości, ile razy coś wystąpi w zbiorze możliwych wyników. Jest to reprezentacja szans na coś się dzieje. Prawdopodobieństwo 1 oznacza, że coś się wydarzy, ale prawdopodobieństwo 0 oznacza, że coś się nie wydarzy.

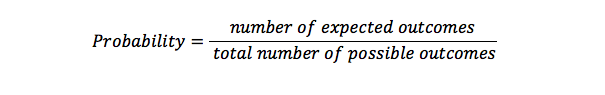
Równanie kwadratowe

wzór wyrażony jako:

x = −B ± √B2-4AC/2A

wzór odległości

wzór jest używany przy obliczaniu odległości między dwoma punktami na płaszczyźnie współrzędnych. Wzór jest wyrażony jako:

d=√(x₁ – x₂)2 + (y₁ – y₂)2

nachylenie wzór

nachylenie jest miarą zmian linii wyrażoną jako dzielenie zmiany osi Y przez zmianę na osi X (wzrost/bieg).

na przykład, jeśli masz punkt A (X1, Y1) i B (X2, Y2), możesz obliczyć nachylenie jako:

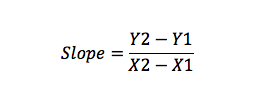
punkt przecięcia stoku Formula_8071

punkt przecięcia stoku jest równaniem liniowym wyrażonym jako Y = MX+b, w którym:

• M oznacza nachylenie linii, podczas gdy b jest punktem przecięcia osi Y, gdzie punkt przecięcia osi Y przecina oś Y.
• jeśli linia przejdzie przez początek, to punkt przecięcia osi y wynosi zero, A równanie będzie wyrażone jako Y = MX.

formuła punktu środkowego

jest to formuła, która znajduje punkt środkowy linii. Na przykład, jeśli masz dwa punkty, A (X1, Y1) i B (X2, Y2), wtedy punkt środkowy będzie równy:

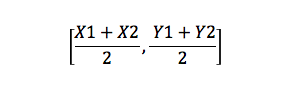
Powierzchnia trójkąta

wzór wyrażony jako ½ (podstawa x wysokość) jest używany do obliczenia całkowitego obszaru zamkniętego w trójkącie.

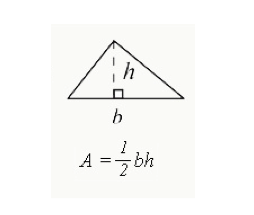
• b = podstawa trójkąta (krawędź jednego boku)
• h=wysokość trójkąta. Wysokość dla trójkąta prostokątnego będzie bokiem o kącie 90 stopni. W przypadku innych trójkątów wysokość spadnie do wnętrza trójkąta, jak pokazano powyżej.

Twierdzenie Pitagorasa

twierdzenie Pitagorasa jest kluczowe przy obliczaniu nieznanego boku trójkąta prostokątnego, gdy znane są dwa boki. Wzór wyraża się jako a2+b2=c2. Suma dwóch krótszych boków jest równa sumie dłuższego boku.

Powierzchnia prostokąta i obwodu

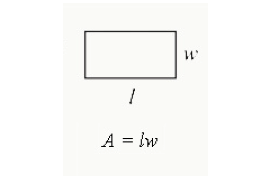
aby znaleźć pole prostokąta, należy pomnożyć długość przez szerokość. Jest to całkowita powierzchnia zamknięta w prostokącie.

Area = Length x Width

z drugiej strony, obwód prostokąta to odległość wokół niego.

obwód = (L + W + L + W) uproszczony jako 2 (L + W)

objętość prostopadłościanu

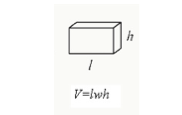
objętość prostopadłościanu można obliczyć mnożąc jego długość, szerokość i wysokość.

obszar okręgu

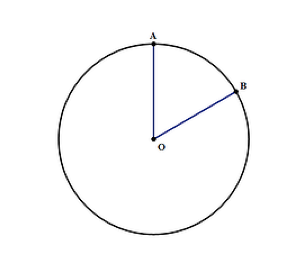
obszar okręgu można znaleźć za pomocą wzoru nr2, gdzie:

• π jest stałą zapisaną jako 3.14, co jest ważne, aby pamiętać, jeśli nie będziesz miał kalkulatora podczas testu
• r-to promień okręgu, jak na powyższym schemacie. Jest to odległość od O do krawędzi okręgu w punkcie A lub B

podobnie odległość wokół okręgu jest określana jako obwód. Oblicza się ją jako:

Obwód okręgu = nD lub 2nr

gdzie:

• D, czyli średnica jest dwukrotnie większa od promienia okręgu. Jest to linia, która dzieli okrąg na dwie połowy dotykając dwóch końców okręgu.

wzory trygonometryczne Sinus (SOH), Cosinus (CAH), tangens (Toa)

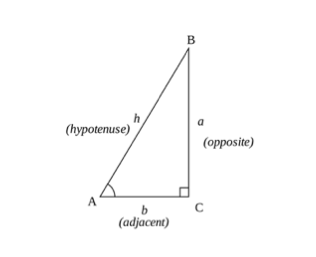
obliczenia trygonometryczne można sumować za pomocą podstawowych pojęć trójkąta za pomocą reguł sinusa, cosinusa i stycznej (SOHCAHTOA). Możesz obliczyć cosinus, sinus lub styczną kąta używając boków trójkąta.

gdzie:

• bok przeciwny – jest bokiem trójkąta, który jest przeciwny do kąta ()
• bok przylegający-jest bokiem, który jest najbliższy kątowi, ale nie najdłuższy bok.
• przeciwprostokątna jest najdłuższym bokiem trójkąta.

Wskazówki dotyczące zapamiętywania formuł i równań matematycznych aktu

aby zapamiętać formuły podczas egzaminu ACT, ważne jest, aby zapoznać się wcześnie, czytając obszary tematyczne określone dla testu matematycznego.

Możesz również ćwiczyć, próbując jak najwięcej problemów, aby opanować formułę.

używanie różnych kanałów, takich jak mówienie formułek głośniej lub pisanie ich na wykresach i trzymanie ich w pokoju, może pomóc Ci zapamiętać formuły.