rozszerzalności liniowej, rozszerzalności powierzchni i objętości lub sześcienności są wszystkie parametry, które są regulowane przez energię cieplną. Wszystkie trzy parametry zależą od wzrostu temperatury, który jest przede wszystkim w jednostce temperatury Celsjusza.
rozszerzalność liniowa dodatkowo zależy od oryginalnej długości i końcowej długości, rozszerzalność powierzchni dodatkowo zależy od oryginalnej powierzchni i końcowej powierzchni, a na koniec, rozszerzalność sześcienna lub objętościowa zależy od oryginalnej objętości i końcowej objętości.
wzór na obliczenie ekspansywności liniowej wynosi (l2-l1) / l1θ
l2 reprezentuje długość końcową.
l1 reprezentuje pierwotną długość.
θ oznacza wzrost temperatury w stopniach Celsjusza.
wzór na obliczenie rozszerzalności powierzchni to (A2-A1) / A1θ
A2 oznacza powierzchnię końcową.
A1 reprezentuje pierwotny obszar.
θ oznacza wzrost temperatury w stopniach Celsjusza.
wzór na obliczenie objętości lub sześcienności wynosi (V2-V1) / V1θ
V2 oznacza objętość końcową.
V1 reprezentuje oryginalny wolumin.
θ oznacza wzrost temperatury w stopniach Celsjusza.
rozwiążmy trzy przykłady na liniową ekspansywność, ekspansywność powierzchni i objętość lub sześcienność odpowiednio. Encyklopedia kalkulatora (Nickzom Calculator) jest w stanie rozwiązać te parametry pokazując działanie formuły i dokładnie odpowiedzieć.
przede wszystkim trzeba mieć dostęp do kalkulatora Nickzom za pomocą dowolnego z tych środków:
- www– https://www.nickzom.org/calculator-plus
- Android (płatny) – https://play.google.com/store/apps/details?id=org.nickzom.nickzomcalculator
- Apple (płatne) – https://itunes.apple.com/us/app/nickzom-calculator/id1331162702?mt=8
następnie przejdź do mapy kalkulatora, kliknij na energię cieplną w sekcji Fizyka
przykład 1:
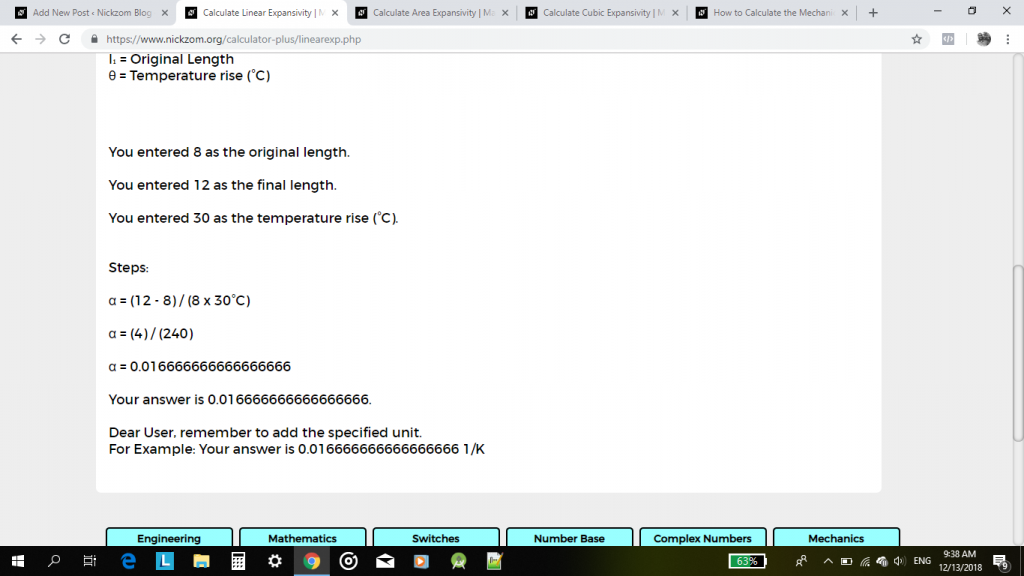
Znajdź liniową ekspansywność (α) metalu, gdzie jego pierwotna długość wynosi 8 cm, a jego końcowa długość wynosi 12 cm po przejściu wzrostu temperatury o 20°C.
α = (l2-l1) / l1θ
gdzie:
L2 (Długość końcowa) = 12 cm
L1 (Długość pierwotna) = 8 cm
θ (wzrost temperatury) = 20°C
α = (12 – 8) / 8(20) 1/°C
α = 4 / 160 1/°c
α = 0.025 1 / °C
używając kalkulatora Nickzom, kliknij na ekspansywność liniową,
następnie wprowadź wartości odpowiednio i dokładnie
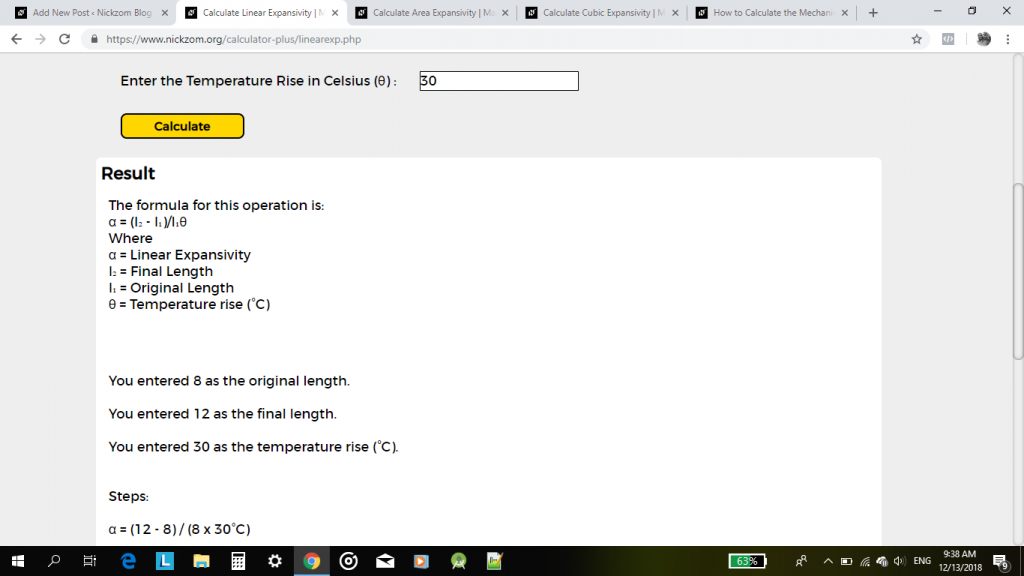
na koniec kliknij przycisk Oblicz
przykład 2:
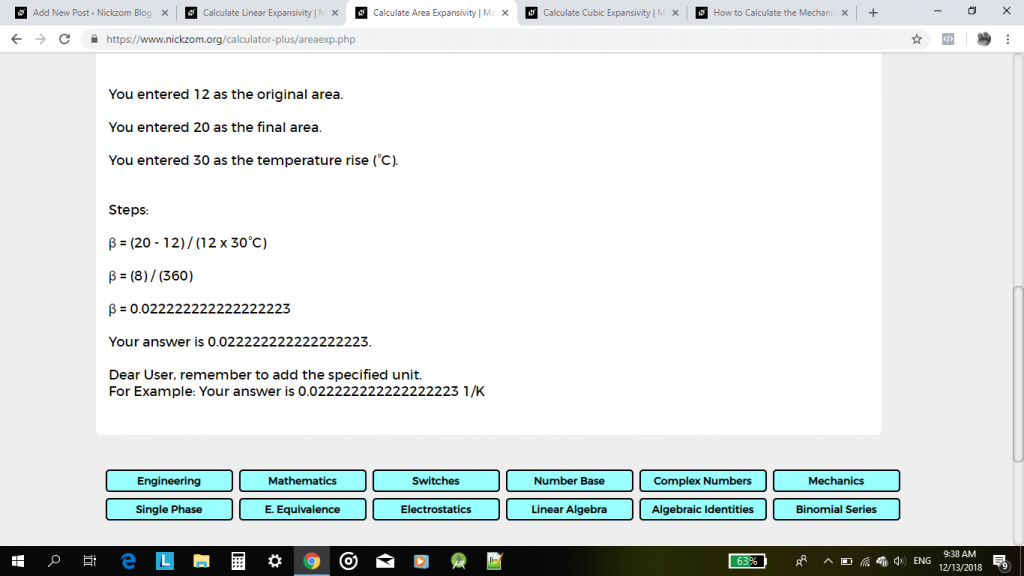
Znajdź ekspansywność powierzchni (β) metalu, gdzie jego pierwotny obszar wynosi 12 cm2, a jego końcowa długość wynosi 20 cm2 po przejściu wzrostu temperatury o 30°C.
β = (A2 – A1) / a1θ
gdzie:
A2 (końcowy obszar) = 20 cm2
A1 (pierwotny obszar) = 12 cm2
θ (wzrost temperatury) = 30°C
,
β = (20 – 12) / 12(30) 1/°C
β = 8 / 360 1/°c
β = 0.02222 1 / °C
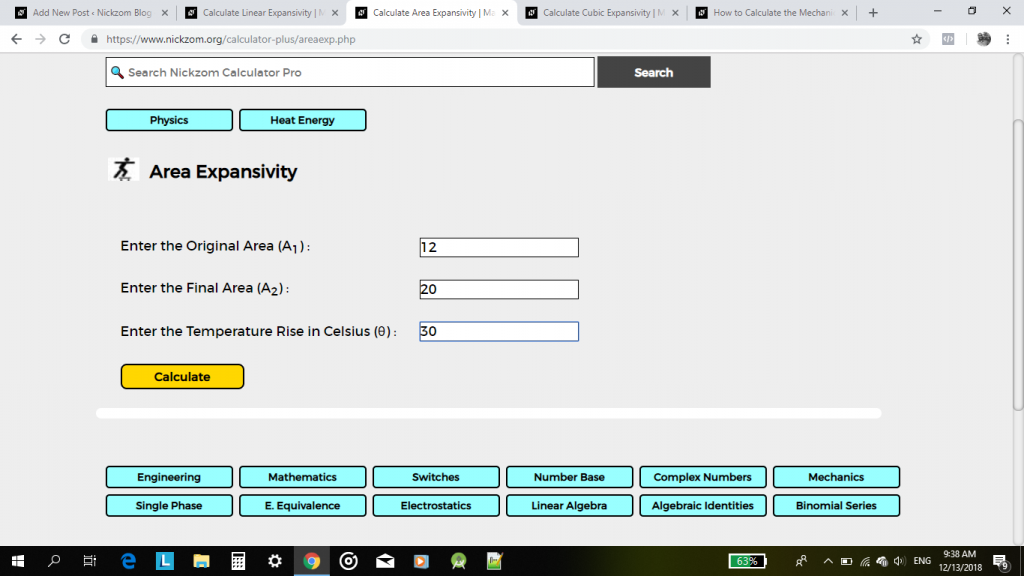
korzystając z kalkulatora Nickzom, kliknij na rozszerzalność obszaru,

następnie wprowadź wartości odpowiednio i dokładnie
na koniec kliknij przycisk Oblicz

przykład 3:
Znajdź objętość lub sześcienność (γ) metalu, gdzie jego pierwotna objętość wynosi 18 cm3, a jego ostateczna długość wynosi 30 cm3 po przejściu wzrostu temperatury o 50°C.
γ = (V2-V1) / V1θ
gdzie:
v2 (objętość końcowa) = 18 cm3
V1 (objętość oryginalna) = 30 cm3
θ (wzrost temperatury) = 50°C