Diffie-Hellman

Como pode, duas pessoas em uma sala lotada de derivar um segredo que apenas o par de saber, sem revelar o segredo a alguém que pode estar a ouvir?

esse é exatamente o cenário que a troca de chaves Diffie-Hellman existe para resolver.

a troca de chaves Diffie-Hellman é um meio para duas partes estabelecerem conjuntamente um segredo compartilhado sobre um canal inseguro, sem ter nenhum conhecimento prévio uma da outra.

eles nunca realmente trocam o segredo, apenas alguns valores que combinam, o que lhes permite atingir o mesmo valor resultante.Conceitualmente, a melhor maneira de visualizar a troca de chaves Diffie-Hellman é com a onipresente demonstração de mistura de cores de tinta. Vale a pena revisá-lo rapidamente se você não estiver familiarizado com ele.

no entanto, neste artigo, queremos dar um passo adiante e realmente mostrar a matemática na troca de chaves Diffie-Hellman.

DH Math

Antes de entrar na matemática de Diffie-Hellman, você vai querer ter uma compreensão básica do que é um número primo e qual é a operação do módulo (também conhecido como divisão restante). Ambos os termos foram definidos em outro artigo.

abaixo está um infográfico descrevendo todas as etapas da troca Diffie-Hellman entre Alice e Bob.

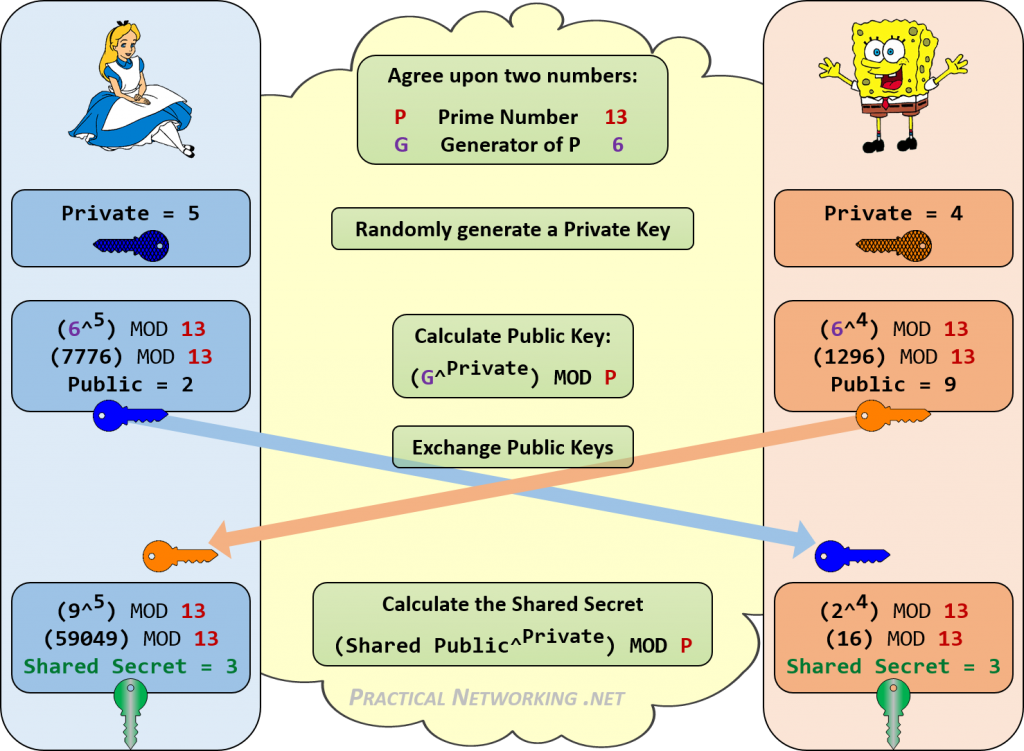
Observe como ambos Alice e Bob foram capazes de atingir o mesmo Segredo Compartilhado de 3. Qualquer pessoa que ouvisse sua troca de chaves DH só conheceria os valores públicos e os valores p E G iniciais. Não há maneira consistente de combinar esses números (13, 6, 2, 9) para atingir 3.

números DH

em nosso exemplo, usamos um número primo de 13. Como esse número primo também é usado como módulo para cada cálculo, todo o espaço-chave para o segredo compartilhado resultante só pode ser 0-12. Quanto maior esse número, mais difícil será o tempo que um invasor terá em brute forçando seu segredo compartilhado.Obviamente, estávamos usando números muito pequenos acima para ajudar a manter a matemática relativamente simples. As verdadeiras trocas de DH estão fazendo matemática em números que são muito maiores. Existem três tamanhos típicos para os números em Diffie-Hellman:

Os bits de tamanho é uma referência para o Primeiro número. Isso equivale diretamente a todo o espaço-chave do segredo compartilhado resultante. Para ter uma ideia do tamanho desse espaço-chave:

para escrever um número de 768 bits, você precisaria de 232 dígitos decimais.
para escrever completamente um número de 1024 bits, você precisaria de 309 dígitos decimais.
para escrever completamente um número de 1536 bits, você precisaria de 463 dígitos decimais.

usando o segredo compartilhado

uma vez que o segredo compartilhado foi atingido, ele normalmente se torna usado no cálculo para estabelecer uma chave de criptografia simétrica conjunta e/ou uma chave HMAC conjunta – também conhecida como chaves de sessão.

mas é importante ressaltar que o próprio segredo compartilhado não deve ser usado diretamente como chave secreta. Se fosse, tudo o que você pode ter certeza é que ao longo da conversa segura você ainda está falando com a mesma parte que estava do outro lado da troca Diffie-Hellman.

no entanto, você ainda não tem confirmação ou garantia de quem é a outra parte. Só que ninguém mais pode, de repente, fingir ser eles no meio de sua conversa segura.

a geração das chaves de sessão reais deve incluir o segredo compartilhado DH, junto com algum outro valor que só seria conhecido pela outra parte pretendida, como algo do esquema de autenticação que você escolheu.

prefere conteúdo de vídeo a texto? A maior parte deste artigo foi gravada e pode ser visualizada no Youtube:

exemplo de navegação em série RSA > >