Diffie-Hellman

Cum pot doi oameni într-o cameră aglomerată să obțină un secret pe care numai perechea îl știe, fără a dezvălui secretul nimănui care ar putea asculta?

acesta este exact scenariul pe care există schimbul de chei Diffie-Hellman pentru a-l rezolva.

schimbul de chei Diffie-Hellman este un mijloc pentru două părți de a stabili împreună un secret comun pe un canal nesigur, fără a avea cunoștințe prealabile unul despre celălalt.

nu schimbă niciodată secretul, ci doar câteva valori pe care ambele le combină și care le permit să atingă aceeași valoare rezultată.

conceptual, cel mai bun mod de a vizualiza schimbul de chei Diffie-Hellman este cu demonstrația omniprezentă de amestecare a culorilor vopselei. Merită să o revizuiți rapid dacă nu sunteți familiarizați cu aceasta.

cu toate acestea, în acest articol vrem să facem un pas mai departe și să vă arătăm de fapt matematica în schimbul de chei Diffie-Hellman.

DH Math

înainte de a intra în matematica lui Diffie-Hellman, veți dori să aveți o înțelegere de bază a ceea ce este un număr prim și care este operația modulului (aka, Divizia rest). Ambii termeni au fost definiți într-un alt articol.

mai jos este un infografic care prezintă toate etapele schimbului Diffie-Hellman între Alice și Bob.

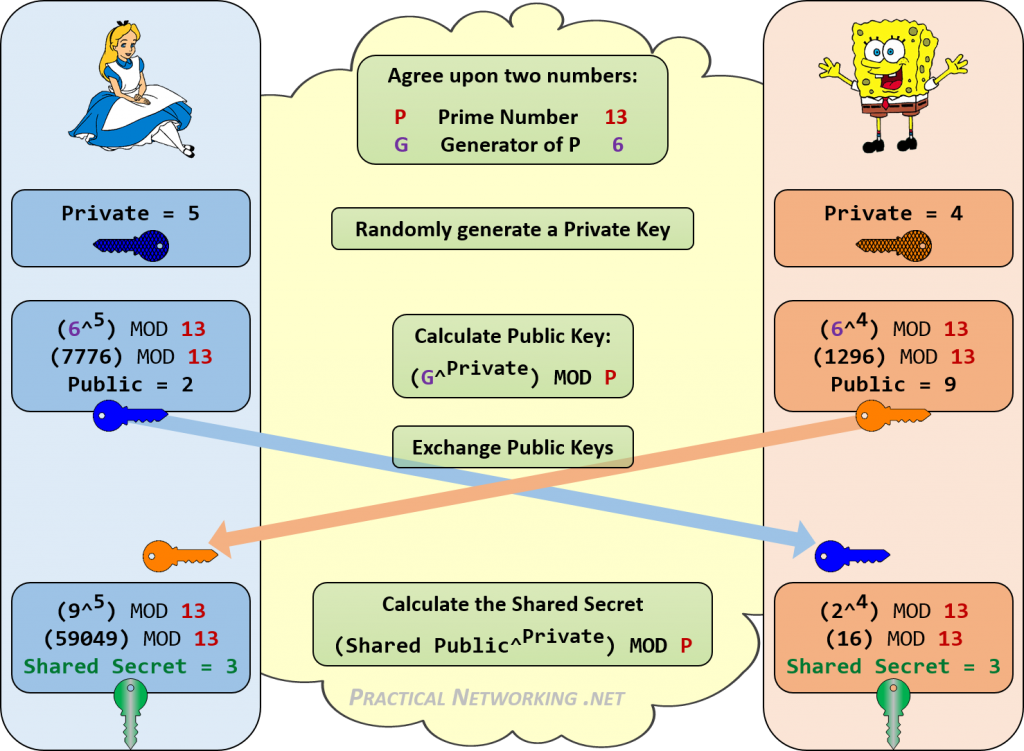
observați cum atât Alice, cât și Bob au reușit să obțină același Secret comun al lui 3. Oricine ascultă schimbul de chei DH ar cunoaște doar valorile publice și valorile inițiale P și G. Nu există o modalitate consecventă de a combina aceste numere (13, 6, 2, 9) pentru a atinge 3.

numere DH

în exemplul nostru, am folosit un număr prim de 13. Deoarece acest număr prim este, de asemenea, utilizat ca modul pentru fiecare calcul, întregul spațiu cheie pentru secretul partajat rezultat poate fi doar 0-12. Cu cât acest număr este mai mare, cu atât va fi mai dificil un timp pe care un atacator îl va avea în forțarea brută a secretului dvs. comun.

evident, am folosit numere foarte mici de mai sus pentru a menține matematica relativ simplă. Adevăratele schimburi DH fac matematică pe numere care sunt mult mai mari. Există trei dimensiuni tipice pentru numerele din Diffie-Hellman:

dimensiunea bitului este o referință la numărul prim. Acest lucru echivalează direct cu întregul spațiu cheie al secretului comun rezultat. Pentru a vă face o idee despre cât de mare este acest spațiu cheie:

pentru a scrie complet un număr de 768 biți, veți avea nevoie de 232 de cifre zecimale.
pentru a scrie complet un număr de 1024 biți, veți avea nevoie de 309 cifre zecimale.
pentru a scrie complet un număr de 1536 biți, veți avea nevoie de 463 de cifre zecimale.

utilizarea Secretului partajat

odată ce secretul partajat a fost atins, acesta devine de obicei utilizat în calcul pentru a stabili o cheie de criptare simetrică comună și/sau o cheie HMAC comună – cunoscută și sub numele de chei de sesiune.

dar este important să subliniem că secretul partajat în sine nu ar trebui folosit direct ca cheie secretă. Dacă ar fi, tot ce puteți fi siguri este că pe parcursul conversației sigure vorbiți în continuare cu aceeași parte care a fost de cealaltă parte a schimbului Diffie-Hellman.

cu toate acestea, încă nu aveți nicio confirmare sau asigurare cu privire la cine este cealaltă parte. Doar că nimeni altcineva nu poate dintr-o dată pretinde a fi ei în mijlocul conversației sigure.

generarea cheilor de sesiune reale ar trebui să includă secretul partajat DH, împreună cu o altă valoare care ar fi cunoscută doar celeilalte părți intenționate, cum ar fi ceva din schema de autentificare pe care ați ales-o.

preferați conținutul video decât textul? Majoritatea acestui articol a fost înregistrat și poate fi vizualizat pe Youtube:

seria de navigare RSA exemplu > >