jaké ACT matematické vzorce by měli studenti vědět a tipy, jak si je zapamatovat?
část ACT Math obsahuje 60 otázek s pěti možnostmi výběru, na které by studenti měli odpovědět během 60 minut. Otázky jsou čerpány ze šesti tematických oblastí pokrytých až do 11.ročníku. Zahrnují Pre-algebru, střední algebru, elementární algebru, souřadnicovou geometrii, trigonometrii a rovinnou geometrii.
zde jsou témata a dovednosti zahrnuté v testu Math ACT.
Algebra
sekce obsahuje 14 otázek a testuje studenta na desetinných místech, celých číslech, zlomcích, poměru, kladných celočíselných mocninách, celých číslech, odmocninách, procentech a proporcích. Mezi další testovaná témata patří jedna proměnná, lineární rovnice, absolutní hodnota, násobky a faktory, medián, průměr, režim, interpretace dat a počítání problémů a pravděpodobnosti.
Intermediate Algebra
tato část obsahuje devět otázek testujících studenta v nerovnostech, absolutní hodnota, kvadratický vzorec, systémy rovnice, racionální a radikální výrazy, funkce, kvadratické nerovnosti, polynomy, matice a komplexní čísla.
elementární Algebra
v oblasti se bude týkat asi deset otázek týkajících se polynomů, proměnných, faktoringu, celočíselných exponentů, odmocnin, lineárních nerovností a kvadratických rovnic.
geometrie roviny
budete mít 14 otázek, které se dotýkají rovinných postav, jako jsou obdélníky, rovnoběžníky, trojúhelníky, lichoběžníky a kruhy. Některé otázky testují znalosti o kolmých čarách, rotacích, 3D geometrii, ploše, obvodu, logickém uvažování, objemu, překladech a odrazech.
souřadnicová geometrie
bude kolem devíti otázek z plošného testování na grafu bodů, grafů číselných čar, kruhů, polynomů, čar, křivek, středového vzorce, kuželů, transformací, vzorce vzdálenosti, rovnic a vztahů grafů, sklonu a vlastností kolmých a rovnoběžných čar.
v sekci trigonometrie najde čtyři otázky týkající se trigonometrických funkcí, rovnic a identit, trigonometrických poměrů pravoúhlého trojúhelníku a modelování trigonometrických funkcí.
seznam Act matematických vzorců
zde je seznam 13 ACT matematických vzorců, které potřebujete vědět pro test ACT:
- aritmetický průměr
- Pravděpodobnost
- kvadratická rovnice
- vzorec vzdálenosti
- vzorec svahu
- vzorec pro zachycení svahu
- středový vzorec
- plocha trojúhelníku
- Pythagorova věta
- plocha obdélníku a obvodu
- objem trojúhelníku kvádr
- plocha kruhu
- trigonometrické vzorce
aritmetický průměr
Toto je stejné jako průměr a je to součet všech položek děleno počtem položek. Například při výpočtu průměru hodnot jste vydělili součet počtem hodnot
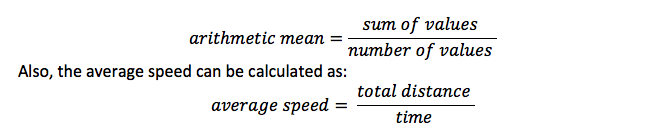
pravděpodobnostní vzorec
Pravděpodobnost se používá při výpočtu možnosti, kolikrát se něco stane v sadě možných výsledků. Je to reprezentace šancí, že se něco stane. Pravděpodobnost 1 znamená, že se něco stane, ale možnost 0 znamená, že se něco nestane.
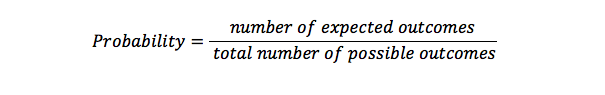
kvadratická rovnice
vzorec vyjádřený jako:
x = – b ± √b2-4ac / 2a
používá se k určení x-zachycení parabolické nebo kvadratické rovnice.
vzorec vzdálenosti
vzorec se používá při výpočtu vzdálenosti mezi dvěma body v rovině souřadnic. Vzorec je vyjádřen jako:
d=√(x₁-x₂) 2 + (y₁ – y₂)2
vzorec svahu
sklon je měřítkem změn čáry vyjádřených jako změna osy Y děleno změnou na ose X (vzestup/běh).
například, pokud máte bod a (X1, Y1) a B (X2, Y2), pak můžete vypočítat sklon jako:
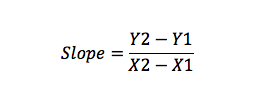
vzorec pro zachycení svahu
vzorec pro zachycení svahu je přímková rovnice vyjádřená jako Y=MX+b, ve které:
- M znamená sklon čáry, zatímco b je y-intercept, kde y-intercept bod protíná osu y.
- pokud čára projde počátkem, pak je y-intercept nulový a rovnice bude vyjádřena jako Y=MX.
středový vzorec
Toto je vzorec, který najde střed řádku. Například, pokud máte dva body, A (X1, Y1) a B (X2, Y2), pak střed bude:
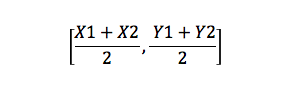
plocha trojúhelníku
vzorec vyjádřený jako ½ (základna x výška) se používá k výpočtu celkové plochy uzavřené v trojúhelníku.
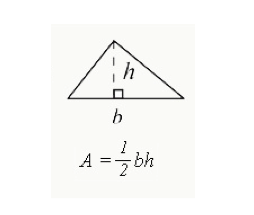
- b= základna trojúhelníku (okraj jedné strany)
- h=výška trojúhelníku. Výška pravoúhlého trojúhelníku bude strana s úhlem 90 stupňů. U ostatních trojúhelníků bude výška klesat po vnitřku trojúhelníku, jak je znázorněno výše.
Pythagorova věta
Pythagorova věta je rozhodující při výpočtu neznámé strany pravoúhlého trojúhelníku, pokud jsou známy dvě strany. Vzorec je vyjádřen jako a2+b2=c2. Součet dvou kratších stran se rovná součtu delší strany.

plocha obdélníku a obvodu
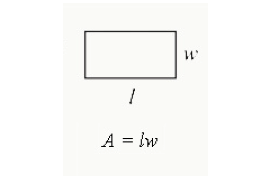
Chcete-li najít oblast obdélníku, vynásobíte délku šířkou. Je to celková plocha uzavřená v obdélníku.
Area = délka x šířka
na druhé straně obvod obdélníku je vzdálenost kolem něj.
Perimeter = (L+W+L+W) zjednodušený jako 2 (L+W)
objem kvádru
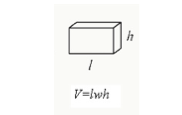
objem kvádru můžete vypočítat vynásobením jeho délky, šířky a výšky kvádru.
plocha kruhu
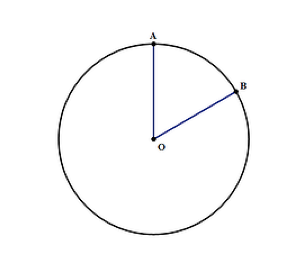
oblast kruhu lze nalézt pomocí vzorce nr2, kde:
- π je konstanta, která je zapsána jako 3.14, což je důležité mít na paměti, pokud nebudete mít kalkulačku během testu
- r-je poloměr kruhu, jako ve výše uvedeném diagramu. Je to Vzdálenost od O k okraji kružnice v bodě a nebo B
podobně se vzdálenost kolem kružnice označuje jako obvod. Vypočítá se jako:
obvod kruhu = nD nebo 2nr
kde:
- D, což je průměr je dvojnásobek poloměru kružnice. Je to čára, která rozděluje kruh na dvě poloviny dotýkající se dvou konců kruhu.
trigonometrické vzorce sinus (SOH), kosinus (CAH), tečna (TOA)
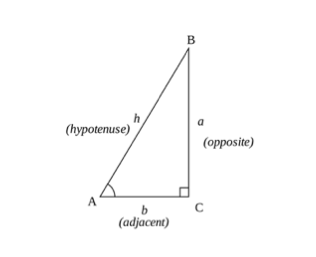
trigonometrické výpočty lze shrnout podle základních pojmů trojúhelníku pomocí sinusových, kosinových a tečných pravidel (SOHCAHTOA). Můžete vypočítat kosinus, sinus nebo tečnu úhlu pomocí stran trojúhelníku.

kde:
- opačná strana-je strana trojúhelníku, která je protilehlá k úhlu ()
- sousední strana-je strana, která je nejblíže k úhlu, ale ne nejdelší strana.
- přepona je nejdelší stranou trojúhelníku.
Tipy pro zapamatování matematických vzorců a rovnic Act
Chcete-li si zapamatovat vzorce během zkoušky ACT, je důležité se brzy seznámit čtením v tematických oblastech určených pro matematický test.
můžete také cvičit pokusem o co nejvíce problémů, abyste zvládli vzorec.
použití různých kanálů, jako je vyslovení vzorců hlasitěji nebo jejich psaní na grafech a lepení ve vašem pokoji, vám pomůže zapamatovat si vzorce.