Diffie-Hellman

jak mohou dva lidé v přeplněné místnosti odvodit tajemství, které zná jen pár, aniž by odhalil tajemství komukoli jinému, kdo by mohl poslouchat?

to je přesně ten scénář, který má Diffie-Hellmanova výměna klíčů vyřešit.

výměna klíčů Diffie-Hellman je prostředkem pro dvě strany, aby společně vytvořily sdílené tajemství přes nezabezpečený kanál, aniž by o sobě měly předchozí znalosti.

nikdy si nevyměňují tajemství, jen některé hodnoty, které oba kombinují a které jim umožňují dosáhnout stejné výsledné hodnoty.

koncepčně je nejlepším způsobem, jak vizualizovat výměnu klíčů Diffie-Hellman, všudypřítomná demonstrace míchání barev. Pokud s tím nejste obeznámeni, vyplatí se to rychle zkontrolovat.

v tomto článku však chceme jít o krok dále a skutečně vám ukázat matematiku ve výměně klíčů Diffie-Hellman.

DH Math

než se dostanete do matematiky Diffie-Hellman, budete chtít mít základní znalosti o tom, co je prvočíslo a co je operace modulu (aka, zbytek divize). Oba tyto pojmy byly definovány v jiném článku.

níže je infographic popisující všechny kroky Diffie-Hellman výměny mezi Alice a Bob.

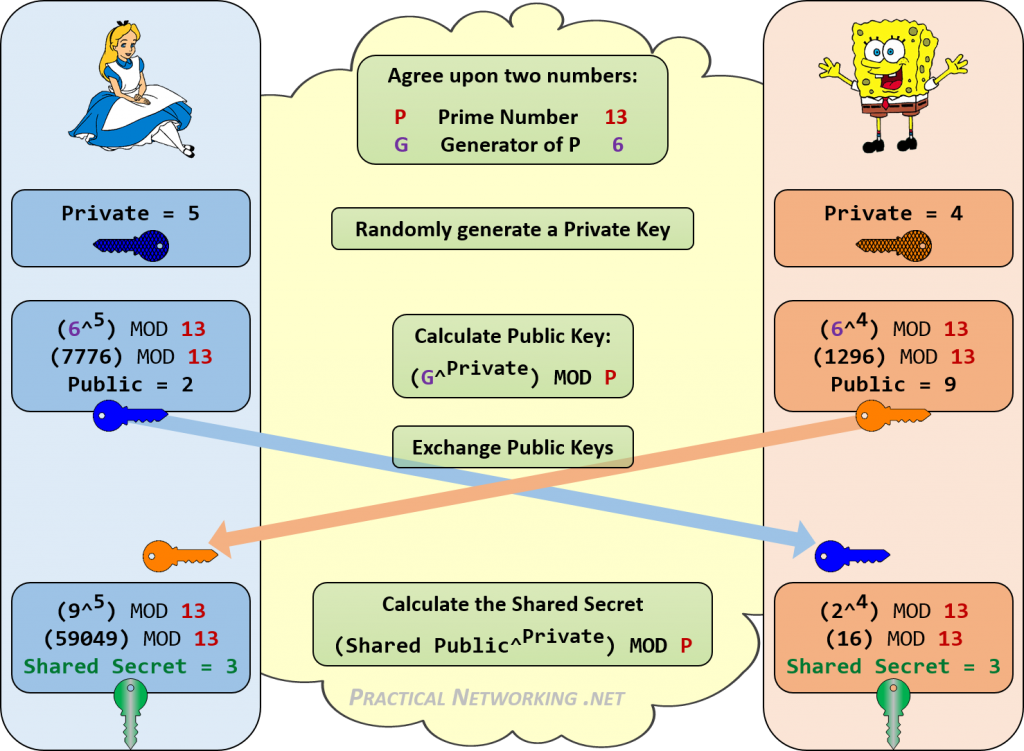
Všimněte si, jak Alice a Bob byli schopni dosáhnout stejné sdílené tajemství 3. Každý, kdo poslouchá jejich výměnu klíčů DH, by znal pouze veřejné hodnoty, a počáteční hodnoty P A G. Neexistuje žádný konzistentní způsob, jak kombinovat tato čísla (13, 6, 2, 9) k dosažení 3.

DH čísla

v našem příkladu jsme použili prvočíslo 13. Vzhledem k tomu, že toto prvočíslo je také použito jako modul pro každý výpočet, celý klíčový prostor pro výsledné sdílené tajemství může být vždy pouze 0-12. Čím větší je toto číslo, tím obtížnější bude mít útočník v hrubém vynucení vašeho sdíleného tajemství.

je zřejmé, že jsme používali velmi malá čísla výše, abychom pomohli udržet matematiku relativně jednoduchou. Skutečné DH výměny dělají matematiku na číslech, která jsou mnohem větší. Existují tři typické velikosti čísel v Diffie-Hellman:

bitová velikost je odkazem na prvočíslo. To se přímo rovná celému klíčovému prostoru výsledného sdíleného tajemství. Abychom vám poskytli představu o tom, jak velký je tento klíčový prostor:

abyste mohli plně napsat 768 bitové číslo, potřebujete 232 desetinných číslic.
abyste mohli plně napsat 1024 bitové číslo, potřebujete 309 desetinných číslic.
abyste mohli plně napsat 1536 bitové číslo, potřebujete 463 desetinných číslic.

použití sdíleného tajemství

jakmile je sdíleného tajemství dosaženo, obvykle se používá při výpočtu k vytvoření společného symetrického šifrovacího klíče a / nebo společného klíče HMAC-známého také jako klíče relace.

je však důležité zdůraznit, že samotné sdílené tajemství by nemělo být přímo používáno jako tajný klíč. Pokud ano, vše, co si můžete být jisti, je, že během bezpečné konverzace stále mluvíte se stejnou stranou, která byla na druhé straně výměny Diffie-Hellman.

stále však nemáte žádné potvrzení nebo ujištění o tom, kdo je druhá strana. Jen to, že nikdo jiný nemůže najednou předstírat, že je uprostřed vaší bezpečné konverzace.

generování skutečných klíčů relace by mělo zahrnovat sdílené tajemství DH spolu s nějakou jinou hodnotou, která by byla známa pouze zamýšlené druhé straně, jako něco z vybraného schématu ověřování.

preferujete videoobsah před textem? Většina tohoto článku byla zaznamenána a lze ji zobrazit na Youtube:

řada navigace RSA příklad >>