hvilke ACT Math formler skal eleverne vide og Tips til at huske dem?
ACT Math sektion består af 60 fem-multi-choice spørgsmål, som eleverne skal svare på inden for 60 minutter. Spørgsmålene er hentet fra seks emneområder dækket op til 11.klasse. De omfatter Pre-algebra, mellemliggende algebra, elementær algebra, Koordinere Geometri, Trigonometri og plane geometri.
her er de emner og færdigheder, der er omfattet af Math ACT-testen.
Algebra
sektionen består af 14 spørgsmål og tester den studerende på decimaler, hele tal, fraktioner, forhold, positive heltalskræfter, heltal, kvadratrødder, procentdel og andel. Andre testede emner inkluderer en variabel, lineære ligninger, absolut værdi, multipla og faktorer, median, middelværdi, tilstand, datatolkning og tælleproblemer og sandsynlighed.
mellemliggende Algebra
denne del består af ni spørgsmål, der tester den studerende i uligheder, absolut værdi, kvadratisk formel, ligningssystemer, rationelle og radikale udtryk, funktioner, kvadratiske uligheder, polynomer, matricer og komplekse tal.
elementær Algebra
der vil være omkring ti spørgsmål i området, der berører polynomer, variabler, factoring, heltalseksponenter, firkantede rødder, lineære uligheder og kvadratiske ligninger.
Plangegeometri
du vil have 14 spørgsmål, der berører plane figurer som rektangler, parallelogrammer, trekanter, trapesoider og cirkler. Nogle spørgsmål tester viden om vinkelrette linjer, rotationer, 3D geometri, Område, Omkreds, logisk ræsonnement, volumen, oversættelser og refleksioner.
Koordinatgeometri
der vil omkring ni spørgsmål fra områdetestningen på grafen over punkter, tallinjegrafer, cirkler, polynomer, linjer, kurver, midtpunktsformel, Konik, transformationer, afstandsformel, ligninger og grafforhold, hældning og egenskaber for vinkelrette og parallelle linjer.
i afsnittet finder Trigonometri fire spørgsmål om trigonometriske funktioner, ligninger og identiteter, højre trekant trigonometriske forhold og trigonometriske funktioner modellering.
liste over ACT Math-formler
her er en liste over 13 ACT math-formler, du har brug for at vide til ACT-testen:
- aritmetisk gennemsnit
- Sandsynlighed
- kvadratisk ligning
- Afstandsformel
- Hældningsformel
- Hældningsafskæringsformel
- Midtpunktsformel
- areal af en trekant
- Pythagoras sætning
- areal af rektangel og omkreds
- volumen af kuboid
- areal af en cirkel
- trigonometriske formler
aritmetisk gennemsnit
dette er det samme som gennemsnittet, og det er summen af en cirkel alle varer divideret med antallet af varer. For eksempel ved beregning af gennemsnittet af værdier dividerede du summen med antallet af værdier
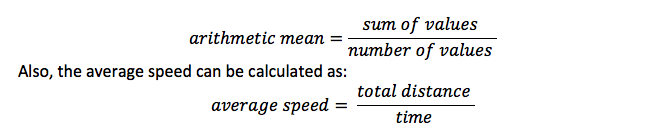
Sandsynlighedsformel
Sandsynlighed bruges til beregning af muligheden for antallet af gange, der vil forekomme noget i et sæt mulige resultater. Det er en repræsentation af chancerne for, at der sker noget. En sandsynlighed på 1 betyder, at der er et bestemt noget, der vil ske, men en mulighed for 0 betyder, at noget ikke vil ske.
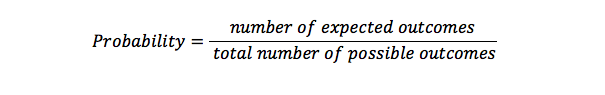
kvadratisk ligning
formlen udtrykt som:
H = −B B2-4ac/2A
det bruges til at bestemme h-aflytningerne af en parabolisk eller kvadratisk ligning.
Afstandsformel
formlen bruges ved beregning af afstanden mellem to punkter på et koordinatplan. Formlen er udtrykt som:
d=l – 2 + (yrun – y₂)2
Hældningsformel
hældningen er et mål for linjeændringer udtrykt som y-akseændringen divideres med ændringen på H-aksen (stigning/løb).
for eksempel, hvis du har punkt A (H1, Y1) og B (H2, Y2), kan du beregne hældning som:
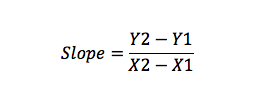
Hældningsafskæringsformel
hældningsafskæringsformlen er en linjeligning udtrykt som Y=MH+b, hvor:
- M står for linjens hældning, mens b er y-skæringspunktet, hvor y-skæringspunktet krydser y-aksen.
- hvis linjen passerer gennem oprindelsen, er y-skæringspunktet nul, og ligningen udtrykkes som Y=MH.
Midtpunktsformel
dette er en formel, der finder midtpunktet for en linje. For eksempel, hvis du har to punkter, A (1, Y1) og B (2, Y2), vil midtpunktet være:
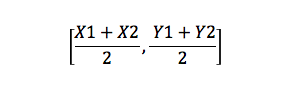
arealet af en trekant
formlen udtrykt som basishøjde bruges til at beregne det samlede areal indesluttet i en trekant.
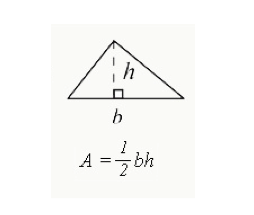
- B= bunden af trekanten (kanten af den ene side)
- h=højden af en trekant. Højden for en retvinklet trekant vil være siden med en 90 graders vinkel. For andre trekanter vil højden falde ned i det indre af trekanten, som vist ovenfor.
Pythagoras sætning
Pythagoras sætning er afgørende ved beregning af en retvinklet trekants ukendte side, når to sider er kendt. Formlen udtrykkes som a2 + b2=c2. Summen af to kortere sider er lig med summen af den længere side.

område af rektangel og omkreds
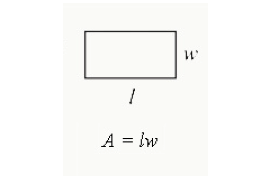
for at finde et rektangelområde multiplicerer du længden med bredden. Det er det samlede areal indesluttet i et rektangel.
område = længde * bredde
på den anden side er et rektangels omkreds afstanden omkring det.
Perimeter = (L+B+L+B) forenklet som 2 (L+B)
volumen af kuboid
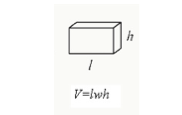
du kan beregne en cuboid volumen ved at gange dens længde, bredde og højde af cuboid.
område af en cirkel
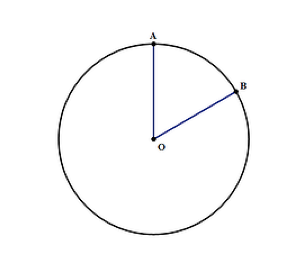
en cirkels område kan findes ved hjælp af formlen nr2 hvor:
- Kris er en konstant, der er skrevet som 3.14, hvilket er vigtigt at huske, om du ikke har en lommeregner under testen
- r-er cirkelens radius, som i diagrammet ovenfor. Det er afstanden fra O til kanten af cirklen ved punkt A eller B
tilsvarende betegnes afstanden omkring cirklen som omkredsen. Det beregnes som:
cirkelens omkreds = nD eller 2nr
hvor:
- D, som er diameteren er to gange cirkelens radius. Det er den linje, der deler cirklen i to halvt rørende to ender af en cirkel.
trigonometriske formler sinus (SOH), cosinus (CAH), Tangent (TOA)
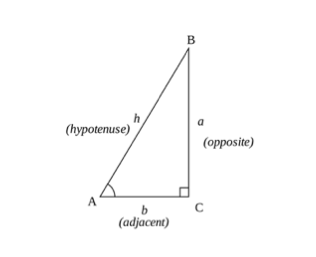
trigonometriske beregninger kan opsummeres ved grundlæggende begreber i en trekant ved hjælp af sinus -, cosinus-og tangentreglerne (SOHCAHTOA). Du kan beregne cosinus, sinus eller tangent af en vinkel ved hjælp af en trekants sider.

hvor:
- modsatte side-er trekantens side, der er modsat vinklen ()
- tilstødende side-er den side, der er tættest på vinklen, men ikke den længste side.
- hypotenusen er trekantens længste side.
Tips til at huske ACT Math formler og ligninger
for at huske formlerne under ACT eksamen er det vigtigt at gøre dig bekendt tidligt ved at læse i de emneområder, der er angivet til matematikprøven.
du kan også øve dig ved at prøve så mange problemer som muligt for at mestre formlen.
brug af forskellige kanaler som at sige formlerne højere eller skrive dem på diagrammer og stikke dem i dit værelse kan hjælpe dig med at huske formlerne.