Diffie-Hellman

Hvordan kan to personer i et overfyldt rum udlede en hemmelighed, som kun parret kender, uden at afsløre hemmeligheden for nogen anden, der måske lytter?

det er netop det scenario, som Diffie-Hellman-Nøgleudvekslingen eksisterer for at løse.

Diffie-Hellman-Nøgleudvekslingen er et middel for to parter til i fællesskab at etablere en delt hemmelighed over en usikker kanal uden at have nogen forudgående kendskab til hinanden.

de udveksler faktisk aldrig hemmeligheden, bare nogle værdier, som begge kombinerer, som lader dem opnå den samme resulterende værdi.

konceptuelt er den bedste måde at visualisere Diffie-Hellman-Nøgleudvekslingen med den allestedsnærværende malingsfarveblandingsdemonstration. Det er værd at hurtigt gennemgå det, hvis du ikke er bekendt med det.

men i denne artikel ønsker vi at gå et skridt videre og faktisk vise dig matematikken i Diffie-Hellman-Nøgleudvekslingen.

DH Math

før du kommer ind i Diffie-Hellmans matematik, vil du have en grundlæggende forståelse af, hvad et primtal er, og hvad Modulusoperationen er (aka, resten division). Begge disse udtryk er defineret i en anden artikel.

nedenfor er en infografik, der beskriver alle trin i Diffie-Hellman-udvekslingen mellem Alice og Bob.

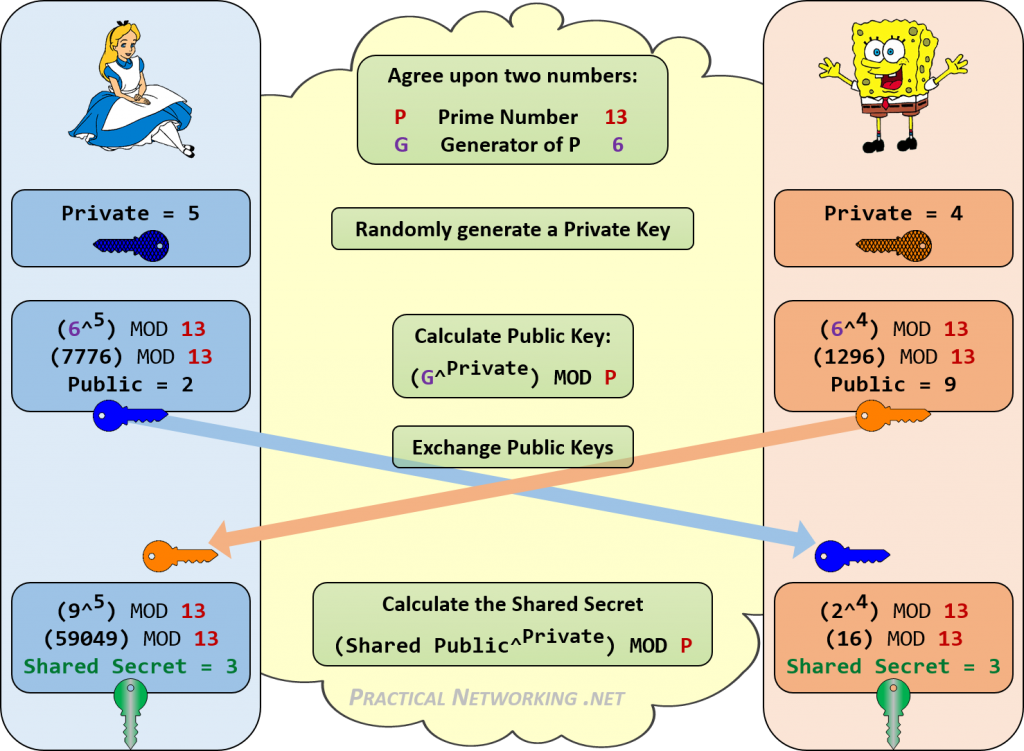
Læg mærke til, hvordan både Alice og Bob var i stand til at opnå den samme delte hemmelighed af 3. Enhver, der lytter ind på deres DH-nøgleudveksling, ville kun kende de offentlige værdier og de startende P-og G-værdier. Der er ingen konsekvent måde at kombinere disse tal (13, 6, 2, 9) for at opnå 3.

DH-numre

i vores eksempel brugte vi et primtal på 13. Da dette primtal også bruges som modul for hver beregning, kan hele nøglepladsen for den resulterende delte hemmelighed kun være 0-12. Jo større dette tal er, jo vanskeligere en gang en angriber vil have i brute, der tvinger din delte hemmelighed.

vi brugte naturligvis meget små tal ovenfor for at hjælpe med at holde matematikken relativt enkel. Ægte DH-udvekslinger laver matematik på tal, der er meget større. Der er tre typiske størrelser til tallene i Diffie-Hellman:

bitstørrelsen er en henvisning til primtal. Dette svarer direkte til hele nøgleområdet for den resulterende delte hemmelighed. For at give dig en ide om, hvor stort dette nøgleområde er:

for fuldt ud at skrive et 768 bit nummer, skal du bruge 232 decimaler.
for fuldt ud at skrive et 1024 bit nummer, skal du bruge 309 decimaler.
for fuldt ud at skrive et 1536 bit nummer, skal du bruge 463 decimaler.

brug af den delte hemmelighed

når den delte hemmelighed er nået, bruges den typisk i beregningen til at etablere en fælles symmetrisk krypteringsnøgle og/eller en fælles HMAC – nøgle-også kendt som sessionsnøgler.

men det er vigtigt at påpege, at selve den delte hemmelighed ikke direkte skal bruges som den hemmelige nøgle. Hvis det var, alt hvad du kan være sikker på er, at du i hele den sikre samtale stadig taler til den samme fest, der var på den anden side af Diffie-Hellman-udvekslingen.

du har dog stadig ingen bekræftelse eller sikkerhed for, hvem den anden part er. Bare at ingen andre pludselig kan foregive at være dem midt i din sikre samtale.

genereringen af de faktiske sessionsnøgler skal indeholde DH-delt hemmelighed sammen med en anden værdi, der kun ville være kendt for den tilsigtede anden part, som noget fra det godkendelsesskema, du valgte.

foretrækker videoindhold frem for tekst? Størstedelen af denne artikel er optaget og kan ses på Youtube:

serie Navigation RSA eksempel >>