Welche ACT Math Formulas sollten die Schüler kennen und Tipps zum Auswendiglernen?
ACT Math Abschnitt umfasst 60 Fünf-Multi-Choice-Fragen, die Schüler innerhalb von 60 Minuten beantworten sollten. Die Fragen stammen aus sechs Themenbereichen, die bis zur 11. Sie umfassen Voralgebra, Zwischenalgebra, Elementaralgebra, Koordinatengeometrie, Trigonometrie und Ebenengeometrie.
Hier sind die Themen und Fähigkeiten, die im Math ACT-Test behandelt werden.
Algebra
Der Abschnitt umfasst 14 Fragen und testet die Schüler auf Dezimalstellen, ganze Zahlen, Brüche, Verhältnis, positive ganze Potenzen, ganze Zahlen, Quadratwurzeln, Prozentsatz und Anteil. Weitere getestete Themen sind eine Variable, lineare Gleichungen, absoluter Wert, Vielfache und Faktoren, Median, Mittelwert, Modus, Dateninterpretation sowie Zählprobleme und Wahrscheinlichkeit.
Intermediate Algebra
Dieser Teil besteht aus neun Fragen, die den Schüler in Ungleichungen, Absolutwerten, quadratischen Formeln, Gleichungssystemen, rationalen und radikalen Ausdrücken, Funktionen, quadratischen Ungleichungen, Polynomen, Matrizen und komplexen Zahlen testen.
Elementare Algebra
In diesem Bereich werden rund zehn Fragen zu Polynomen, Variablen, Factoring, ganzzahligen Exponenten, Quadratwurzeln, linearen Ungleichungen und quadratischen Gleichungen gestellt.
Ebene Geometrie
Sie haben 14 Fragen zu ebenen Figuren wie Rechtecken, Parallelogrammen, Dreiecken, Trapezen und Kreisen. Einige Fragen testen das Wissen über senkrechte Linien, Rotationen, 3D-Geometrie, Fläche, Umfang, logisches Denken, Volumen, Übersetzungen und Reflexionen.
Koordinatengeometrie
Es wird rund neun Fragen aus dem Bereich Prüfung auf dem Diagramm der Punkte, Anzahl Liniendiagramme, Kreise, Polynome, Linien, Kurven, Mittelpunkt Formel, Kegel, Transformationen, Distanzformel, Gleichungen und Diagrammbeziehungen, Steigung und Eigenschaften von senkrechten und parallelen Linien.
Im Abschnitt Trigonometrie finden Sie vier Fragen zu trigonometrischen Funktionen, Gleichungen und Identitäten, trigonometrischen Verhältnissen des rechtwinkligen Dreiecks und zur Modellierung trigonometrischer Funktionen.
Liste der ACT Math-Formeln
Hier ist eine Liste von 13 ACT Math-Formeln, die Sie für den ACT-Test kennen müssen:
- Arithmetisches Mittel
- Wahrscheinlichkeit
- Quadratische Gleichung
- Entfernungsformel
- Steigungsformel
- Steigungsabschnittsformel
- Mittelpunktformel
- Fläche eines Dreiecks
- Satz des Pythagoras
- Fläche des Rechtecks und Umfangs
- Volumen des Quaders
- Fläche eines Kreises
- Trigonometrische Formeln
Arithmetisches Mittel
Dies ist das gleiche wie der Durchschnitt, und es ist die Summe von allen Elementen durch die Anzahl der Elemente geteilt. Wenn Sie beispielsweise den Durchschnitt der Werte berechnen, teilen Sie die Summe durch die Anzahl der Werte
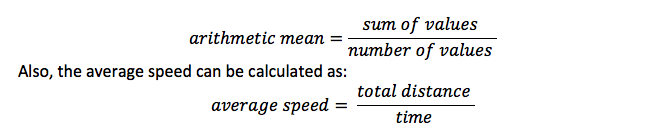
Wahrscheinlichkeitsformel
Die Wahrscheinlichkeit wird verwendet, um die Möglichkeit zu berechnen, wie oft etwas in einer Reihe möglicher Ergebnisse auftritt. Es ist eine Darstellung der Chancen, dass etwas passiert. Eine Wahrscheinlichkeit von 1 bedeutet, dass etwas Bestimmtes passieren wird, aber eine Möglichkeit von 0 bedeutet, dass etwas nicht passieren wird.
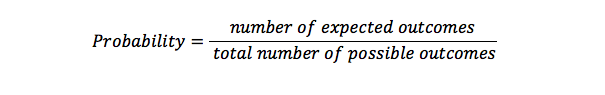
Quadratische Gleichung
Die Formel ausgedrückt als:
x = -b ± √b2-4ac /2a
Es wird verwendet, um die x-Abschnitte einer parabolischen oder quadratischen Gleichung zu bestimmen.
Entfernungsformel
Die Formel wird verwendet, wenn der Abstand zwischen zwei Punkten auf einer Koordinatenebene berechnet wird. Die Formel wird ausgedrückt als:
d=√(x₁ – x₂) 2 + (y₁ – y₂) 2
Steigungsformel
Die Steigung ist ein Maß für Linienänderungen, ausgedrückt als Änderung der Y-Achse dividiert durch die Änderung auf der X-Achse (Anstieg / Lauf).
Wenn Sie beispielsweise Punkt A (X1, Y1) und B(X2, Y2) haben, können Sie die Steigung wie folgt berechnen:
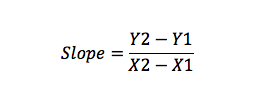
Slope Intercept Formula
Die Slope-Intercept-Formel ist eine Liniengleichung, ausgedrückt als Y=MX+b, in der:
- M steht für die Steigung der Linie, während b der y-Schnittpunkt ist, an dem der y-Schnittpunkt die y-Achse kreuzt.
- Wenn die Linie durch den Ursprung verläuft, ist der y-Achsenabschnitt Null und die Gleichung wird als Y=MX ausgedrückt.
Mittelpunktformel
Dies ist eine Formel, die den Mittelpunkt einer Linie ermittelt. Wenn Sie beispielsweise zwei Punkte haben, A (X1, Y1) und B (X2, Y2), lautet der Mittelpunkt:
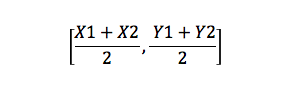
Fläche eines Dreiecks
Die als ½ (Basis x Höhe) ausgedrückte Formel wird verwendet, um die in einem Dreieck eingeschlossene Gesamtfläche zu berechnen.
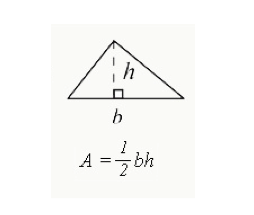
- b= die Basis des Dreiecks (der Rand einer Seite)
- h=die Höhe eines Dreiecks. Die Höhe für ein rechtwinkliges Dreieck ist die Seite mit einem 90-Grad-Winkel. Bei anderen Dreiecken fällt die Höhe wie oben gezeigt im Inneren des Dreiecks ab.
Satz des Pythagoras
Der Satz des Pythagoras ist entscheidend für die Berechnung der unbekannten Seite eines rechtwinkligen Dreiecks, wenn zwei Seiten bekannt sind. Die Formel wird ausgedrückt als a2+b2= c2. Die Summe zweier kürzerer Seiten ist gleich der Summe der längeren Seite.

Fläche von Rechteck und Umfang
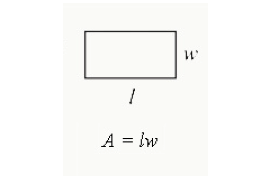
Um die Fläche eines Rechtecks zu ermitteln, multiplizieren Sie die Länge mit der Breite. Es ist die Gesamtfläche, die in einem Rechteck eingeschlossen ist.
Fläche = Länge x Breite
Andererseits ist der Umfang eines Rechtecks der Abstand um es herum.
Umfang = (L + W+L+W) vereinfacht als 2(L+W)
Volumen des Quaders
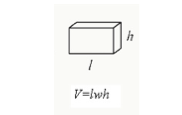
Sie können das Volumen eines Quaders berechnen, indem Sie seine Länge, Breite und Höhe des Quaders multiplizieren.
Fläche eines Kreises
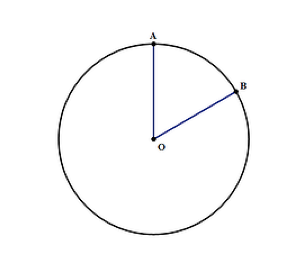
Die Fläche eines Kreises kann mit der Formel nr2 ermittelt werden, wobei:
- π ist eine Konstante, die als 3 geschrieben wird.14, was wichtig ist, wenn Sie während des Tests keinen Taschenrechner haben
- r- ist der Radius des Kreises, wie im obigen Diagramm. Es ist der Abstand von O zum Rand des Kreises am Punkt A oder B
In ähnlicher Weise wird der Abstand um den Kreis als Umfang bezeichnet. Es wird berechnet als:
Umfang des Kreises = nD oder 2nr
Wobei:
- D, das heißt, der Durchmesser ist doppelt so groß wie der Radius des Kreises. Es ist die Linie, die den Kreis in zwei Hälften teilt, die zwei Enden eines Kreises berühren.
Trigonometrische Formeln Sinus (SOH), Cosinus (CAH), Tangens (TOA)
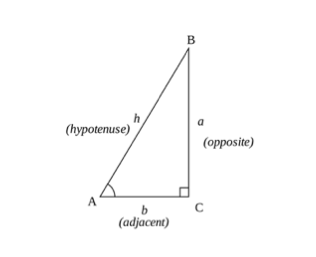
Trigonometrische Berechnungen können durch grundlegende Konzepte eines Dreiecks unter Verwendung der Sinus-, Cosinus- und Tangentenregeln (SOHCAHTOA) summiert werden. Sie können den Kosinus, Sinus oder Tangens eines Winkels anhand der Seiten eines Dreiecks berechnen.

Wo:
- Gegenüberliegende Seite – ist die Seite des Dreiecks, die dem Winkel gegenüberliegt ( )
- Benachbarte Seite – ist die Seite, die dem Winkel am nächsten liegt, aber nicht die längste Seite.
- Die Hypotenuse ist die längste Seite des Dreiecks.
Tipps zum Auswendiglernen von ACT-Matheformeln und -gleichungen
Um sich die Formeln während der ACT-Prüfung zu merken, ist es wichtig, sich frühzeitig mit den für den Mathe-Test angegebenen Themenbereichen vertraut zu machen.
Sie können auch üben, indem Sie so viele Probleme wie möglich versuchen, die Formel zu beherrschen.
Wenn Sie verschiedene Kanäle verwenden, z. B. die Formeln lauter aussprechen oder auf Diagramme schreiben und in Ihr Zimmer kleben, können Sie sich die Formeln besser merken.