Diffie-Hellman

Wie können zwei Personen in einem überfüllten Raum ein Geheimnis ableiten, das nur das Paar kennt, ohne das Geheimnis anderen zu offenbaren, die zuhören könnten?

Das ist genau das Szenario, das der Diffie-Hellman-Schlüsselaustausch lösen soll.

Der Diffie-Hellman-Schlüsselaustausch ist ein Mittel für zwei Parteien, um gemeinsam ein gemeinsames Geheimnis über einen unsicheren Kanal zu etablieren, ohne vorherige Kenntnis voneinander zu haben.

Sie tauschen niemals das Geheimnis aus, sondern nur einige Werte, die beide kombinieren, wodurch sie den gleichen resultierenden Wert erreichen.

Konzeptionell ist der beste Weg, den Diffie-Hellman-Schlüsselaustausch zu visualisieren, die allgegenwärtige Demonstration der Farbmischung von Farben. Es lohnt sich, es schnell zu überprüfen, wenn Sie damit nicht vertraut sind.

In diesem Artikel möchten wir jedoch noch einen Schritt weiter gehen und Ihnen die Mathematik im Diffie-Hellman-Schlüsselaustausch zeigen.

DH Math

Bevor Sie in die Mathematik von Diffie-Hellman einsteigen, sollten Sie ein grundlegendes Verständnis davon haben, was eine Primzahl ist und was die Moduloperation ist (auch bekannt als Restdivision). Beide Begriffe wurden in einem anderen Artikel definiert.

Unten finden Sie eine Infografik, die alle Schritte des Diffie-Hellman-Austauschs zwischen Alice und Bob beschreibt.

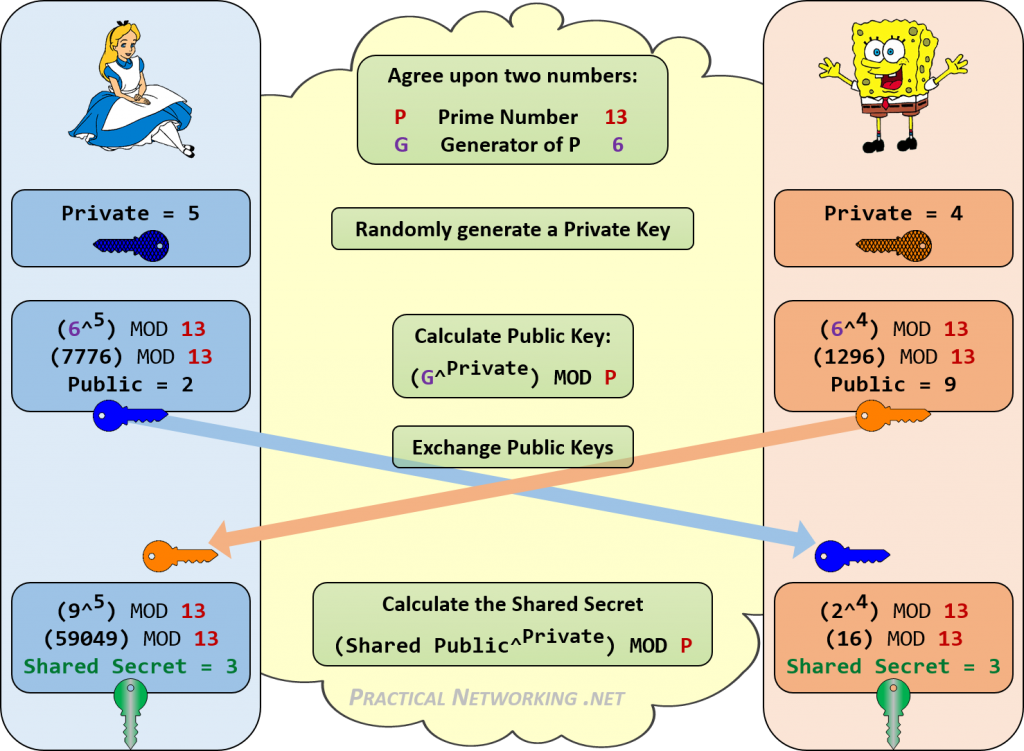
Beachten Sie, wie Alice und Bob dasselbe gemeinsame Geheimnis von 3 erreichen konnten. Jeder, der seinen DH-Schlüsselaustausch mithört, kennt nur die öffentlichen Werte und die P- und G-Startwerte. Es gibt keine konsistente Möglichkeit, diese Zahlen (13, 6, 2, 9) zu kombinieren, um 3 zu erreichen.

Primzahlen

In unserem Beispiel haben wir eine Primzahl von 13 verwendet. Da diese Primzahl auch als Modul für jede Berechnung verwendet wird, kann der gesamte Schlüsselraum für das resultierende gemeinsame Geheimnis immer nur 0-12 sein. Je größer diese Zahl ist, desto schwieriger wird es für einen Angreifer, Ihr gemeinsames Geheimnis brutal zu erzwingen.

Offensichtlich haben wir oben sehr kleine Zahlen verwendet, um die Mathematik relativ einfach zu halten. Wahre DH-Börsen rechnen mit Zahlen, die weitaus größer sind. Es gibt drei typische Größen für die Zahlen in Diffie-Hellman:

Die Bitgröße ist ein Verweis auf die Primzahl. Dies entspricht direkt dem gesamten Schlüsselraum des resultierenden gemeinsamen Geheimnisses. Um Ihnen eine Vorstellung davon zu geben, wie groß dieser Schlüsselraum ist:

Um eine 768-Bit-Zahl vollständig auszuschreiben, benötigen Sie 232 Dezimalstellen.
Um eine 1024-Bit-Zahl vollständig auszuschreiben, benötigen Sie 309 Dezimalstellen.
Um eine 1536-Bit-Zahl vollständig auszuschreiben, benötigen Sie 463 Dezimalstellen.

Verwenden des gemeinsamen Geheimnisses

Sobald das gemeinsame Geheimnis erreicht wurde, wird es typischerweise in der Berechnung verwendet, um einen gemeinsamen symmetrischen Verschlüsselungsschlüssel und /oder einen gemeinsamen HMAC–Schlüssel – auch bekannt als Sitzungsschlüssel – zu etablieren.

Es ist jedoch wichtig darauf hinzuweisen, dass das gemeinsame Geheimnis selbst nicht direkt als geheimer Schlüssel verwendet werden sollte. Wenn es so wäre, können Sie nur sicher sein, dass Sie während des gesamten sicheren Gesprächs immer noch mit derselben Partei sprechen, die sich auf der anderen Seite des Diffie-Hellman-Austauschs befand.

Sie haben jedoch immer noch keine Bestätigung oder Zusicherung, wer die andere Partei ist. Nur dass niemand sonst plötzlich so tun kann, als wäre er mitten in Ihrem sicheren Gespräch.

Die Generierung der tatsächlichen Sitzungsschlüssel sollte das gemeinsame DH-Geheimnis zusammen mit einem anderen Wert enthalten, der nur der beabsichtigten anderen Partei bekannt wäre, z. B. aus dem von Ihnen gewählten Authentifizierungsschema.

Bevorzugen Sie Videoinhalte gegenüber Text? Der Großteil dieses Artikels wurde aufgezeichnet und kann auf Youtube angesehen werden:

Seriennavigation RSA Beispiel >>