Lexikalische Analyse im Compiler-Design

In diesem Artikel diskutieren wir die erste Phase im Compiler-Design, in der das High-Level-Eingabeprogramm in eine Sequenz von Token konvertiert wird. Diese Phase wird als lexikalische Analyse im Compiler-Design bezeichnet.

Inhaltsverzeichnis:

1. Definitionen für die lexikalische Analyse
2. Ein Beispiel für die lexikalische Analyse
3. Architektur des lexikalischen Analysators
4. Reguläre Ausdrücke
5. Endliche Automaten
6. Beziehung zwischen regulären Ausdrücken und endlichen Automaten
7. Längste Übereinstimmungsregel
8. Lexikalische Fehler
9. Fehlerbehebungsschemata
10. Bedarf an lexikalischen Analysatoren
11. Bedarf an lexikalischen Analysatoren

Bei der Lexikalischen Analyse wird eine Zeichenfolge aus einem Quellprogramm konvertiert, die als Eingabe in eine Folge von Token verwendet wird.

Ein lex ist ein Programm, das lexikalische Analysatoren generiert.

Ein lexikalischer Analysator / Lexer /Scanner ist ein Programm, das lexikalische Analysen durchführt.

Die Rollen des lexikalischen Analysators.;

• Lesen von Eingabezeichen aus dem Quellprogramm.
• Korrelation der Fehlermeldungen mit dem Quellprogramm.
• Striping von Leerzeichen und Kommentaren aus dem Quellprogramm.
• Erweiterungsmakros, falls im Quellprogramm gefunden.
• Eingabe identifizierter Token in die Symboltabelle.

Lexem ist eine Instanz eines Tokens, dh eine Folge von Zeichen, die im Quellprogramm gemäß dem Übereinstimmungsmuster eines Tokens enthalten sind.

Ein Beispiel Für den Ausdruck;
c = a + b * 5

Die Lexeme und Token sind;

Lexeme	Token
c	Kennung
=	zuweisungssymbol
eine	Kennung
+	+( Zusatzsymbol)
b	Kennung
*	*( multiplikationssymbol)
5	5( anzahl)

Die vom lexikalischen Analysator erzeugte Sequenz von Token ermöglicht es dem Parser, die Syntax eines programmiersprache.

Ein Token ist eine gültige Zeichenfolge, die von einem Lexem gegeben wird.
In einer Programmiersprache kann dies Folgendes umfassen;

• Schlüsselwörter
• Operatoren
• Interpunktionssymbole
• Konstanten
• Bezeichner
• Zahlen

Ein Muster ist eine Regel, die mit einer Folge von Zeichen (Lexemen) übereinstimmt, die vom Token verwendet werden. Es kann durch reguläre Ausdrücke oder Grammatikregeln definiert werden.

Ein Beispiel für die lexikalische Analyse

Code

#include<iostream>// exampleint main(){ int a, b; a = 7; return 0;}

Token

Lexeme	Token
int	Schlüsselwort
haupt	Schlüsselwort
(	betreiber
)	betreiber
{	betreiber
int	Schlüsselwort
eine	Kennung
,	betreiber
b	Kennung
;	betreiber
eine	Kennung
=	zuweisungssymbol
10	10( anzahl)
;	betreiber
return	Schlüsselwort
0	0( anzahl)
;	Betreiber
}	betreiber

Nicht Tokens

Typ	Token
Präprozessor-Direktive	#include<iostream>
kommentar	// Beispiel

Der Prozess der lexikalischen Analyse besteht aus zwei Phasen.

1. Scannen – Dies beinhaltet das Lesen von Eingabezeichenund Entfernen von Leerzeichen und Kommentaren.
2. Tokenisierung – Dies ist die Produktion von Token als Ausgabe.

Architektur des lexikalischen Analysators

Die Hauptaufgabe des lexikalischen Analysators besteht darin, das gesamte Quellprogramm zu scannen und Token einzeln zu identifizieren.
Scanner sind implementiert, um Token zu erzeugen, wenn sie vom Parser angefordert werden.

Schritte:

1. “ get next token“ wird vom Parser an den lexikalischen Analysator gesendet.
2. Der lexikalische Analysator scannt die Eingabe, bis das „nächste Token“ gefunden ist.
3. Das Token wird an den Parser zurückgegeben.

Reguläre Ausdrücke

Wir verwenden reguläre Ausdrücke, um endliche Sprachen auszudrücken, indem wir Muster für eine endliche Menge von Symbolen definieren.

Durch reguläre Ausdrücke definierte Grammatik wird als reguläre Grammatik bezeichnet, und die durch reguläre Grammatik definierte Sprache wird als reguläre Sprache bezeichnet.
Es gibt algebraische Regeln, die von regulären Ausdrücken befolgt werden, um reguläre Ausdrücke in äquivalente Formen zu manipulieren.

Operationen.

Vereinigung zweier Sprachen A und B wird geschrieben als
A U B = {s | s ist in A oder s ist in B}
Verkettung zweier Sprachen A und B wird geschrieben als
AB = {ss | s ist in A und s ist in B}
Die Kleen-Schließung einer Sprache A wird geschrieben als
A* = Das ist null oder mehr Vorkommen von Sprache A.

Notationen.

Wenn x und y reguläre Ausdrücke sind, die die Sprachen A(x) und B(y) bezeichnen, dann ist
(x) ein regulärer Ausdruck, der A (x) bezeichnet.
Union (x)|(y) ist ein regulärer Ausdruck, der A(x) B(y) bezeichnet.
Concatenation (x)(y) ist ein regulärer Ausdruck, der A(x)B(y) .
Kleen closure (x)* ist ein regulärer Ausdruck, der (A(x))*

Vorrang und Assoziativität bezeichnet.

*‘ Verkettung .‘ und / (pipe) sind links assoziativ.
Kleen closure * hat die höchste Priorität.
Verkettung (.) folgt vorrangig.
(pipe) | hat die niedrigste Priorität.

Repräsentiert gültige Token einer Sprache in regulären Ausdrücken.

X ist ein regulärer Ausdruck, daher;

• x* repräsentiert null oder mehr Vorkommen von x.
• x+ repräsentiert ein oder mehrere Vorkommen von x, dh{x, xx, xxx}
• x? stellt höchstens ein Vorkommen von x dar, dh {x}
• repräsentiert alle Kleinbuchstaben in der englischen Sprache.
• repräsentiert alle Großbuchstaben in der englischen Sprache.
• repräsentiert alle natürlichen Zahlen.

Darstellung des Auftretens von Symbolen mit regulären Ausdrücken
Letter = or
Digit = or |0|1|2|3|4|5|6|7|8|9
Sign =

Darstellung von Sprach-Token mit regulären Ausdrücken.
Dezimal = (Vorzeichen)?(ziffer)+
Identifier = (Buchstabe)(Buchstabe | Ziffer)*

Endliche Automaten

Dies ist die Kombination von fünf Tupeln (Q, Σ, q0, qf, δ), die sich auf Zustände und Übergänge durch Eingabesymbole konzentrieren.
Es erkennt Muster, indem es die Zeichenfolge des Symbols als Eingabe verwendet und seinen Status entsprechend ändert.
Das mathematische Modell für endliche Automaten besteht aus;

• Endlicher Satz von Zuständen (Q)
• Endlicher Satz von Eingabesymbolen (Σ)
• Ein Startzustand (q0)
• Satz von Endzuständen (qf)
• Übergangsfunktion(δ)

Endliche Automaten werden in der lexikalischen Analyse verwendet, um Token in Form von Bezeichnern, Schlüsselwörtern und Konstanten aus dem Eingabeprogramm zu erzeugen.

Endliche Automaten füttern die Zeichenfolge für reguläre Ausdrücke und der Status wird für jedes Literal geändert.

Wenn die Eingabe erfolgreich verarbeitet wurde, erreicht der Automat den Endzustand und wird akzeptiert, andernfalls wird er abgelehnt.

Konstruktion endlicher Automaten

Sei L(r) eine reguläre Sprache durch einige endliche Automaten F(A).

Daher;

• Zustände: Kreise repräsentieren die Zustände von FA und ihre Namen werden in die Kreise geschrieben.
• Startzustand: Dies ist der Zustand, in dem die Automaten starten. Es wird ein Pfeil darauf zeigen.
• Zwischenzustände: Diese haben zwei Pfeile, einer zeigt darauf und der andere zeigt von den Zwischenzuständen aus.
• Endzustand: Von Automaten wird erwartet, dass sie sich im Endzustand befinden, wenn die Eingabezeichenfolge erfolgreich analysiert und durch doppelte Kreise dargestellt wurde. Es kann eine ungerade Anzahl von Pfeilen enthalten, die darauf zeigen, und eine gerade Zahl, die von ihm zeigt, dh
  ungerade Pfeile = gerade Pfeile + 1.
• Übergang: Wenn ein gewünschtes Symbol in der Eingabe gefunden wird, erfolgt der Übergang von einem Zustand in einen anderen Zustand. Die Automaten wechseln entweder in den nächsten Zustand oder bleiben bestehen.
  Ein gerichteter Pfeil zeigt die Bewegung von einem Zustand in einen anderen an, während ein Pfeil auf den Zielzustand zeigt.
  Wenn die Automaten im selben Zustand bleiben, wird ein Pfeil gezeichnet, der von einem Zustand zu sich selbst zeigt.

Ein Beispiel; Angenommen, ein 3-stelliger Binärwert, der auf 1 endet, wird von FA akzeptiert.
Dann FA = {Q(q0, qf), Σ(0,1), q0, qf, δ}

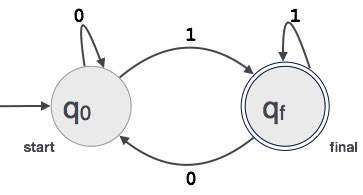
Beziehung zwischen regulären Ausdrücken und endlichen Automaten

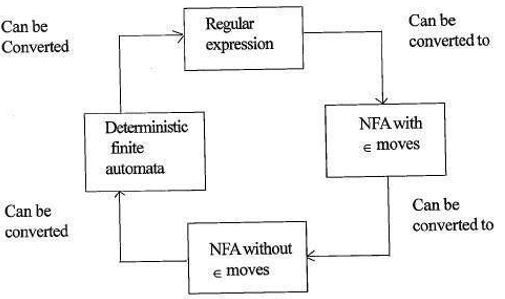
Die Beziehung zwischen regulären Ausdrücken und endlichen Automaten ist wie folgt;
Die folgende Abbildung zeigt, dass es einfach zu konvertieren ist;

• Reguläre Ausdrücke zu nicht-deterministischen endlichen Automaten (NFA) mit ∈ bewegt.
• Nicht-deterministische endliche Automaten mit ∈ bewegt sich zu ohne ∈ bewegt sich
• Nicht-deterministische endliche Automaten ohne ∈ bewegt sich zu deterministischen endlichen Automaten(DFA).
• Deterministische endliche Automaten zu regulären Ausdrücken.

Ein Lex akzeptiert reguläre Ausdrücke als Eingabe und gibt ein Programm zurück, das einen endlichen Automaten simuliert, um die regulären Ausdrücke zu erkennen.
Daher kombiniert lex die Erzeugung von Zeichenfolgenmustern (reguläre Ausdrücke, die die für lex interessanten Zeichenfolgen definieren) und die Zeichenfolgenmustererkennung (ein endlicher Automat, der die interessierenden Zeichenfolgen erkennt).

Längste Übereinstimmungsregel

Sie besagt, dass das gescannte Lexem basierend auf der längsten Übereinstimmung unter allen verfügbaren Token bestimmt werden sollte.
Dies wird verwendet, um Mehrdeutigkeiten bei der Entscheidung über das nächste Token im Eingabestream aufzulösen.
Während der Analyse des Quellcodes scannt der Lexical Analyzer den Code Buchstabe für Buchstabe und entscheidet, ob ein Wort vollständig ist, wenn ein Operator, ein Sonderzeichen oder ein Leerzeichen erkannt wird.

Beispiel:

int intvalue;

Beim Scannen des obigen kann der Analysator nicht feststellen, ob ‚int‘ ein Schlüsselwort int oder das Präfix des Bezeichners intvalue .
Es wird eine Regelpriorität angewendet, bei der ein Schlüsselwort Vorrang vor Benutzereingaben erhält, was bedeutet, dass der Analysator im obigen Beispiel einen Fehler generiert.

Lexikalische Fehler

Ein lexikalischer Fehler tritt auf, wenn eine Zeichenfolge nicht in ein gültiges Token gescannt werden kann.
Diese Fehler können durch eine falsche Schreibweise von Bezeichnern, Schlüsselwörtern oder Operatoren verursacht werden.
Im Allgemeinen werden sehr seltene lexikalische Fehler durch illegale Zeichen in einem Token verursacht.

Fehler können;

• Rechtschreibfehler.
• Transposition von zwei Zeichen.
• Unzulässige Zeichen.
• Überschreitung der Länge des Bezeichners oder der numerischen Konstanten.
• Ersetzen eines Zeichens durch ein falsches Zeichen
• Entfernen eines Zeichens, das vorhanden sein sollte.

Fehlerbehebung.;

• Entfernen eines Zeichens aus der verbleibenden Eingabe
• Transponieren von zwei benachbarten Zeichen
• Löschen eines Zeichens aus der verbleibenden Eingabe
• Einfügen eines fehlenden Zeichens in die verbleibende Eingabe
• Ersetzen eines Zeichens durch ein anderes Zeichen.
• Ignorieren aufeinanderfolgender Zeichen, bis ein legales Token gebildet wird (Wiederherstellung im Panikmodus).

Fehlerwiederherstellungsschemata

Wiederherstellung im Panikmodus.
In diesem Fehlerwiederherstellungsschema werden nicht übereinstimmende Muster aus der verbleibenden Eingabe gelöscht, bis der lexikalische Analysator am Anfang der verbleibenden Eingabe ein wohlgeformtes Token finden kann.
Eine einfachere Implementierung ist für diesen Ansatz von Vorteil.
Es hat die Einschränkung, dass eine große Menge an Eingaben übersprungen wird, ohne auf zusätzliche Fehler zu prüfen.

Lokale Korrektur.
Wenn ein Fehler an einem Punkt erkannt wird, werden Einfüge- / Lösch- und / oder Ersetzungsoperationen ausgeführt, bis ein wohlgeformter Text erreicht ist.
Der Analysator wird mit dem resultierenden neuen Text als Eingabe neu gestartet.

Globale Korrektur.
Es ist eine verbesserte Panikmodus-Wiederherstellung, die bevorzugt wird, wenn die lokale Korrektur fehlschlägt.
Es hat einen hohen Zeit- und Platzbedarf, daher ist es praktisch nicht implementiert.

Bedarf an lexikalischen Analysatoren

1. Verbesserte Compiler-Effizienz – spezielle Puffertechniken zum Lesen von Zeichen beschleunigen den Compiler-Prozess.
2. Einfachheit des Compiler-Designs – Das Entfernen von Leerzeichen und Kommentaren ermöglicht effiziente syntaktische Konstrukte für den Syntaxanalysator.
3. Compiler Portabilität – nur der Scanner kommuniziert mit der Außenwelt.
4. Spezialisierung – Spezielle Techniken können verwendet werden, um den lexikalischen Analyseprozess zu verbessern

Probleme mit der lexikalischen Analyse

1. Lookahead
   Bei einer Eingabezeichenfolge werden Zeichen nacheinander von links nach rechts gelesen.
   Um festzustellen, ob ein Token fertig ist oder nicht, müssen wir das nächste Zeichen betrachten.
   Beispiel: Ist ‚=‘ ein Zuweisungsoperator oder das erste Zeichen im Operator ‚==‘.
   Lookahead überspringt Zeichen in der Eingabe, bis ein wohlgeformtes Token gefunden wird, dies zeigt, dass Look ahead keine signifikanten Fehler abfangen kann, außer für einfache Fehler wie illegale Symbole.
2. Mehrdeutigkeiten
   Die mit lex geschriebenen Programme akzeptieren mehrdeutige Spezifikationen und wählen daher die längste Übereinstimmung, und wenn mehrere Ausdrücke mit der Eingabe übereinstimmen, wird entweder die längste Übereinstimmung bevorzugt oder die erste Regel unter den Übereinstimmungsregeln priorisiert.
3. Reservierte Schlüsselwörter
   Bestimmte Sprachen haben reservierte Wörter, die in anderen Programmiersprachen nicht reserviert sind, z. B. elif ist ein reserviertes Wort in Python, aber nicht in C.
4. Kontextabhängigkeit
   Beispiel:
   Angesichts der Anweisung DO 10 l = 10.86 ist DO10l ein Bezeichner und DO kein Schlüsselwort.
   Und angesichts der Aussage DO 10 l = 10, 86, DO ist ein Schlüsselwort
   Solche Aussagen würden einen erheblichen Blick nach vorne erfordern, um eine Lösung zu finden.

Anwendungen

1. Die von Compilern verwendet werden, erstellen Sie Ihre ausführbaren Binärdateien aus analysiertem Code.
2. Wird von Webbrowsern zum Formatieren und Anzeigen einer Webseite verwendet, die HTML, CSS und Java Script analysiert.

Mit diesem Artikel bei OpenGenus müssen Sie eine starke Vorstellung von der lexikalischen Analyse im Compiler-Design haben.