Résolution de problèmes en faisant une liste

Comme je l’ai mentionné à plusieurs reprises, l’un des principaux objectifs de l’enseignement des mathématiques est d’élever des résolveurs de problèmes confiants. Et bien qu’il existe de nombreuses façons de résoudre les problèmes mathématiques, et que nous, adultes, pouvons souvent considérer les stratégies comme du bon sens, ce sont des choses qui doivent être enseignées. Donner aux enfants autant d’outils que possible les préparera au succès afin que vous puissiez les « libérer » et voir leurs esprits créatifs travailler et explorer. Pour continuer ma série sur l’enseignement aux enfants à la résolution de problèmes, aujourd’hui, je vais discuter de la résolution de problèmes en faisant une liste.

–> Psst! Vos enfants ont-ils besoin d’aide pour comprendre et résoudre des problèmes de mots? Vous aimerez peut-être cet ensemble de modèles de résolution de problèmes de mots modifiables! Utilisez-les avec n’importe quel niveau, pour tout type de problème de mots:

Faire une liste significative:

C’était toujours une approche difficile pour moi personnellement car cela ne semble pas être des mathématiques et peut souvent prendre du temps. Je veux dire, qui veut vraiment s’asseoir et énumérer toutes les solutions possibles à un problème de mathématiques? MAIS, c’est une stratégie très utile, et comme nous le verrons, apprendre à être organisé et systématique est la clé (et permettra également de gagner des tonnes de temps)!

Alors, quand est-il utile de faire une liste? Fondamentalement, chaque fois que vous avez un problème qui a plus d’une solution, ou que vous essayez de résoudre un problème de combinaison, il est utile de faire une liste.

Mais pas n’importe quelle liste de possibilités. Cela vous semblera inutile et frustrant si vous essayez simplement de tirer des possibilités de n’importe où. Et plus que cela, il est très probable que les possibilités seront ignorées ou répétées, ce qui rendra la solution finale erronée.

En plus de cela, il faudra probablement plus de temps pour faire une liste si vous n’avez pas d’approche systématique, ce qui explique probablement pourquoi je n’ai jamais été fan quand j’étais enfant. Personne ne veut simplement s’asseoir et regarder le papier en espérant que des solutions surgiront dans son cerveau.

Organiser les informations de manière logique vous permet de rester sur la bonne voie et garantit que toutes les solutions possibles seront trouvées.

Il existe différentes façons d’organiser l’information, mais l’idée est d’épuiser toutes les possibilités avec une partie de votre liste avant de passer à autre chose.

Par exemple, disons que vous essayez de comprendre toutes les différentes combinaisons de garnitures de crème glacée dans votre magasin de crème glacée local. Ils ont 3 saveurs différentes (chocolat, vanille et fraise), mais ont également 4 garnitures différentes (noix, crème fouettée, bonbons au chocolat et oursons gommeux).

Si vous commencez à énumérer différentes possibilités sans aucune structure, vous risquez de vous perdre dans votre liste et de manquer quelque chose. Donc, à la place, énumérez toutes les possibilités de crème glacée au chocolat avant de passer à la vanille.

Chocolat: juste du chocolat (sans garniture), du chocolat aux noix, du chocolat à la crème fouettée, du chocolat aux bonbons et du chocolat aux oursons gommeux.

Maintenant, nous voyons qu’il y a 5 possibilités si vous obtenez de la glace au chocolat, et nous pouvons donc passer à la vanille, puis à la fraise.

La clé est de commencer par la première saveur et de lister toutes les garnitures possibles dans l’ordre. Passez ensuite à la saveur suivante et parcourez les garnitures dans le même ordre.

Alors rien n’est ignoré, oublié ou répété. Après avoir terminé la liste, nous voyons qu’il y a 15 combinaisons possibles.

Certains étudiants peuvent même remarquer qu’il y aura 5 possibilités pour chaque saveur, et ainsi multiplier 3×5 sans compléter la liste. (C’est une autre excellente stratégie: rechercher des modèles).

Même si un motif n’est pas découvert, cependant, compléter la liste de manière organisée et systématique garantira que toutes les possibilités sont couvertes et que le total (15) est trouvé.

Une autre façon d’organiser la liste consiste à créer un diagramme d’arborescence. Voici un autre exemple de problème:

Sarah est en vacances et a apporté 3 pantalons (bleu, noir et blanc) et 3 chemises (rose, jaune et vert). Combien de combinaisons de tenues différentes peut-elle faire?

L’utilisation d’un diagramme en arbre est un excellent moyen de garder l’information organisée, surtout si vous avez des enfants qui ont du mal à suivre leur liste:

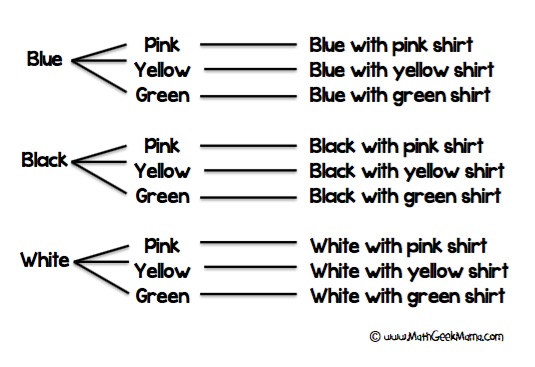
Ensuite, il est très facile pour les étudiants de voir qu’il existe 9 combinaisons de tenues différentes.

Cela vous a-t-il été utile ? Est-ce une stratégie que vous partagez avec vos enfants?

Consultez le reste des articles de cette série et préparez vos enfants à être de grands résolveurs de problèmes:

• Résoudre un problème en Résolvant un Problème Plus Facile
• Résoudre un Problème en Dessinant une Image
• Résoudre un Problème en Travaillant en Arrière
• Résoudre un Problème en Trouvant un Motif
• Résoudre un problème avec Guess & Vérifier