광 ʌv ˌtrɪg.əˈnɒm.ɪ.trik ˈfʌŋk.쩐쨀챌쩌쩌쩔채.
| 삼각 함수의 정확한 값은 실수와 실수의 뿌리를 포함하는 표현을 사용하여 정확하게 표현할 수있는 특정 각도의 삼각 함수의 값입니다. 이 값은 삼각 함수의 분석 값 또는 특수 각도의 삼각 값이라고도합니다. 이 각도는 계산기가 허용되지 않는 테스트에 자주 사용되므로 학생들이 이러한 각도와 이러한 각도의 삼각 함수 값을 암기하는 것이 유용합니다. 이 값을 기억하기위한 니모닉은이 기사의 끝 부분에 있습니다. |
|
||||||||||||||||||||||||||||||||||||||||||||||
니모닉 이 무엇입니까?
특수 각도에 대한 사인 값을 기억하는 니모닉은 다음과 같습니다:

그림 1:특수 각도의 사인에 대한 니모닉
특수 각도의 코사인 값에 대한 니모닉은 유사합니다:

그림 1:특수 각도의 코사인에 대한 니모닉
- 맥아담스,데이비드 전자.. 모든 수학 단어 사전,삼각 함수의 정확한 값. 2 교실 판 20150108-4799968. 74 페이지 인생은 이야기 문제입니다. 2015 년 1 월 8 일. 책
구매
이 문서를 인용:
맥아담스,데이비드 전자. 12/21/2018. 모든 수학 단어 백과 사전. 인생은 이야기 문제입니다. https://www.allmathwords.org/en/e/exactvaltrig.html.
이미지 크레딧
- 모든 이미지와 조작은 달리 명시되지 않는 한 데이비드 맥아담스의 것입니다. 이 응용 프로그램은 당신에게 아름다운 욕실 꾸미기의 갤러리를 보여줍니다.2018 년 12 월 21 일 개정 이력 검토 및 수정. 7/5/2018:깨진 링크 제거,라이센스 업데이트,새로운 마크 업 구현,새로운 지오지브라 프로토콜 구현. (맥아담스,데이비드 이)
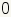
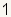
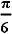 방사선
방사선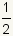
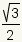
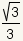
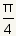 방사선
방사선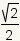
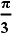 방사선
방사선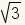
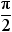 방사선
방사선
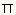 라드
라드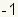
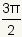 방사선
방사선