welke ACT wiskundige formules moeten studenten kennen en Tips om ze te onthouden?
ACT Math sectie bestaat uit 60 vijf-meerkeuzevragen die studenten binnen 60 minuten moeten beantwoorden. De vragen worden getrokken uit zes thema ‘ s die tot de elfde klas worden behandeld. Ze omvatten Pre-algebra, intermediaire algebra, elementaire algebra, coördinaatmeetkunde, trigonometrie en vlakke meetkunde.
hier zijn de onderwerpen en vaardigheden behandeld op de Math ACT test.
Algebra
de sectie bevat 14 vragen en test de student op decimalen, hele getallen, breuken, ratio, positieve gehele machten, gehele getallen, vierkantswortels, percentage en verhouding. Andere geteste onderwerpen zijn een variabele, lineaire vergelijkingen, absolute waarde, veelvouden en factoren, mediaan, gemiddelde, modus, data interpretatie, en tellen problemen en waarschijnlijkheid.
intermediaire Algebra
dit deel bestaat uit negen vragen die de student toetsen op ongelijkheden, absolute waarde, kwadratische formule, vergelijkingssystemen, rationele en radicale uitdrukkingen, functies, kwadratische ongelijkheden, veeltermen, matrices en complexe getallen.
elementaire Algebra
er zullen ongeveer tien vragen in het gebied zijn die betrekking hebben op veeltermen, variabelen, factoring, integer exponenten, vierkantswortels, lineaire ongelijkheden en kwadratische vergelijkingen.
vlakke geometrie
u zult 14 vragen hebben met betrekking tot vlakke figuren zoals rechthoeken, parallelogrammen, driehoeken, trapezoïden en cirkels. Sommige vragen testen kennis over loodrechte lijnen, rotaties, 3D-geometrie, oppervlakte, omtrek, logisch redeneren, volume, vertalingen en reflecties.
Coördinaatgeometrie
er zullen ongeveer negen vragen uit het gebied testen op de grafiek van punten, getallengrafieken, Cirkels, veeltermen, lijnen, krommen, middenformule, kegelsneden, transformaties, afstandformule, vergelijkingen, en grafiekrelaties, helling en eigenschappen van loodrechte en parallelle lijnen.
in de sectie, Trigonometrie zal vier vragen over trigonometrische functies, vergelijkingen en identiteiten, rechthoekige driehoek trigonometrische ratio ‘ s, en trigonometrische functies modellering.
lijst van wiskundige formules
hier is een lijst van 13 wiskundige formules die u moet weten voor de ACT-test:
- Rekenkundig Gemiddelde
- Waarschijnlijkheid
- Kwadratische Vergelijking
- Afstand Formule
- Helling Formule
- Helling Intercept Formule
- Middelpunt Formule
- Oppervlakte van een Driehoek
- Stelling van Pythagoras
- Oppervlakte van Rechthoek en Omtrek
- Volume van Kubusvormige
- Oppervlakte van een Cirkel
- Goniometrische Formules
Rekenkundig Gemiddelde
Dit is hetzelfde als het gemiddelde, en het is de som van alle posten, gedeeld door het aantal items. Bijvoorbeeld, bij het berekenen van het gemiddelde van waarden, deelt u de som door het aantal waarden
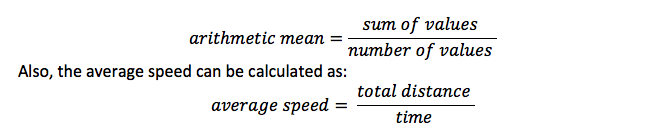
Kansformule
kans wordt gebruikt bij het berekenen van de mogelijkheid van het aantal keren dat er iets zal optreden in een reeks mogelijke resultaten. Het is een weergave van de kans dat er iets gebeurt. Een waarschijnlijkheid van 1 betekent dat er een bepaald iets zal gebeuren, maar een mogelijkheid van 0 betekent dat er iets niet zal gebeuren.
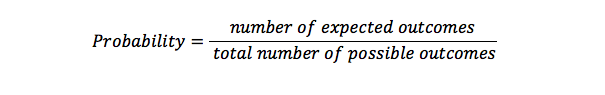
kwadratische vergelijking
de formule uitgedrukt als:
x = – B ± √b2-4AC / 2a
het wordt gebruikt om de x-Onderscheppingen van een parabolische of kwadratische vergelijking te bepalen.
afstand formule
de formule wordt gebruikt bij het berekenen van de afstand tussen twee punten op een coördinatenvlak. De formule wordt uitgedrukt als:
d = √(x₁ – x₂)2 + (y₁ – y₂)2
Hellingsformule
de helling is een maat voor lijnveranderingen, uitgedrukt als de Y-asverandering gedeeld door de verandering op de X-as (stijging/run).
bijvoorbeeld, als u punt A (X1, Y1) en B(X2, Y2), dan kunt u het berekenen van de helling als:
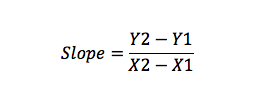
Helling Intercept Formule
De helling-snijpunt formule is een lijn vergelijking uitgedrukt als Y=MX+b in die:
- M staat voor de lijn van de helling, terwijl b is de y-as waar de y-intercept punt kruist de y-as.
- als de lijn door de oorsprong gaat, dan is het y-snijpunt nul en wordt de vergelijking uitgedrukt als Y=MX.
Middenformule
dit is een formule die het midden van een lijn vindt. Bijvoorbeeld, als je twee punten hebt, A (X1, Y1) en B (X2, Y2), dan is het middelpunt:
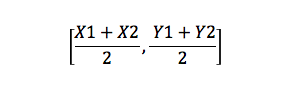
oppervlakte van een driehoek
de formule uitgedrukt als ½ (basis x hoogte) wordt gebruikt om de totale oppervlakte omsloten door een driehoek te berekenen.
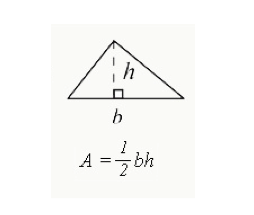
- b = de basis van de driehoek (de rand van een zijde)
- h = de hoogte van een driehoek. De hoogte voor een rechte hoek driehoek zal de zijde met een 90-graden hoek. Voor andere driehoeken zal de hoogte naar beneden vallen het interieur van de driehoek, zoals hierboven weergegeven.
Stelling van Pythagoras
stelling van Pythagoras is cruciaal bij het berekenen van de onbekende zijde van een rechthoekige driehoek wanneer twee zijden bekend zijn. De formule wordt uitgedrukt als a2 + b2=c2. De som van twee kortere zijden is gelijk aan de som van de langere zijde.

oppervlakte van Rechthoek en omtrek
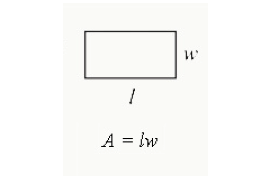
om de oppervlakte van een rechthoek te vinden, vermenigvuldig je de lengte met de breedte. Het is de totale oppervlakte ingesloten in een rechthoek.
Area = Length x Width
aan de andere kant is de omtrek van een rechthoek de afstand eromheen.
Perimeter =(L+W+L + W) vereenvoudigd als 2 (L+W)
Volume van de balk
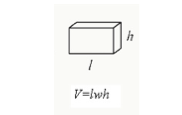
je kunt het volume van een balk berekenen door de lengte, breedte en hoogte van de balk te vermenigvuldigen.
oppervlakte van een cirkel
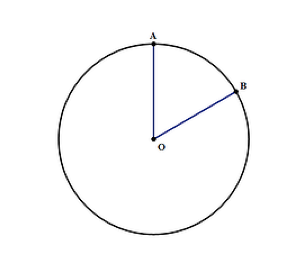
het gebied van een cirkel kan worden gevonden met behulp van de formule nr2 waar:
- π is een constante die wordt geschreven als 3.14, wat belangrijk is om te onthouden als u geen rekenmachine hebt tijdens de test
- r-is de straal van de cirkel, zoals in het diagram hierboven. Het is de afstand van O tot de rand van de cirkel op punt A of B
op dezelfde manier wordt de afstand rond de cirkel aangeduid als de omtrek. Het wordt berekend als:
omtrek van de cirkel = nD of 2nr
waarbij:
- D, dat is de diameter is tweemaal de straal van de cirkel. Het is de lijn die de cirkel verdeelt in twee halve raakt twee uiteinden van een cirkel.
trigonometrische formules sinus (SOH), cosinus (CAH), raaklijn (TOA))
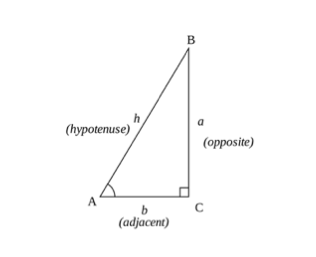
trigonometrische berekeningen kunnen worden opgeteld door basisconcepten van een driehoek met behulp van de sinus -, cosinus-en raakregels (SOHCAHTOA). U kunt de cosinus, sinus of raaklijn van een hoek berekenen met behulp van de zijden van een driehoek.

waarbij:
- tegenoverliggende zijde – is de zijde van de driehoek die tegenovergesteld is aan de hoek ( )
- aangrenzende zijde-is de zijde die het dichtst bij de hoek maar niet de langste zijde.
- de hypotenusa is de langste zijde van de driehoek.
Tips for Memorizing ACT Math Formules and Equations
om de formules te onthouden tijdens het ACT examen, is het belangrijk om jezelf vroeg vertrouwd te maken door te lezen in de onderwerpen die zijn gespecificeerd voor de wiskunde test.
u kunt ook oefenen door zoveel mogelijk problemen te proberen om de formule onder de knie te krijgen.
door verschillende kanalen te gebruiken, zoals de formules harder zeggen of ze op grafieken schrijven en ze in uw kamer plakken, kunt u de formules onthouden.