Diffie-Hellman

Hoe kunnen twee mensen in een drukke kamer een geheim afleiden dat alleen het paar Weet, zonder het geheim te onthullen aan iemand anders die misschien luistert?

dat is precies het scenario dat de Diffie-Hellman sleuteluitwisseling bestaat om op te lossen.

de Diffie-Hellman Key Exchange is een middel voor twee partijen om gezamenlijk een gedeeld geheim over een onveilig kanaal vast te stellen, zonder dat zij elkaar vooraf kennen.

ze wisselen nooit echt het geheim uit, alleen een aantal waarden die beide combineren waardoor ze dezelfde resulterende waarde bereiken.

conceptueel is de beste manier om de Diffie-Hellman-sleuteluitwisseling te visualiseren met de alomtegenwoordige verfkleurmengdemonstratie. Het is de moeite waard om het snel te bekijken als je er niet bekend mee bent.

echter, in dit artikel willen we een stap verder gaan en je de wiskunde laten zien in de Diffie-Hellman sleuteluitwisseling.

DH Math

voordat je in de wiskunde van Diffie-Hellman gaat, wil je een basiskennis hebben van wat een priemgetal is, en wat de Modulus operatie is (ook bekend als Rest division). Beide termen zijn gedefinieerd in een ander artikel.

Hieronder is een infographic met alle stappen van de Diffie-Hellman uitwisseling tussen Alice en Bob.

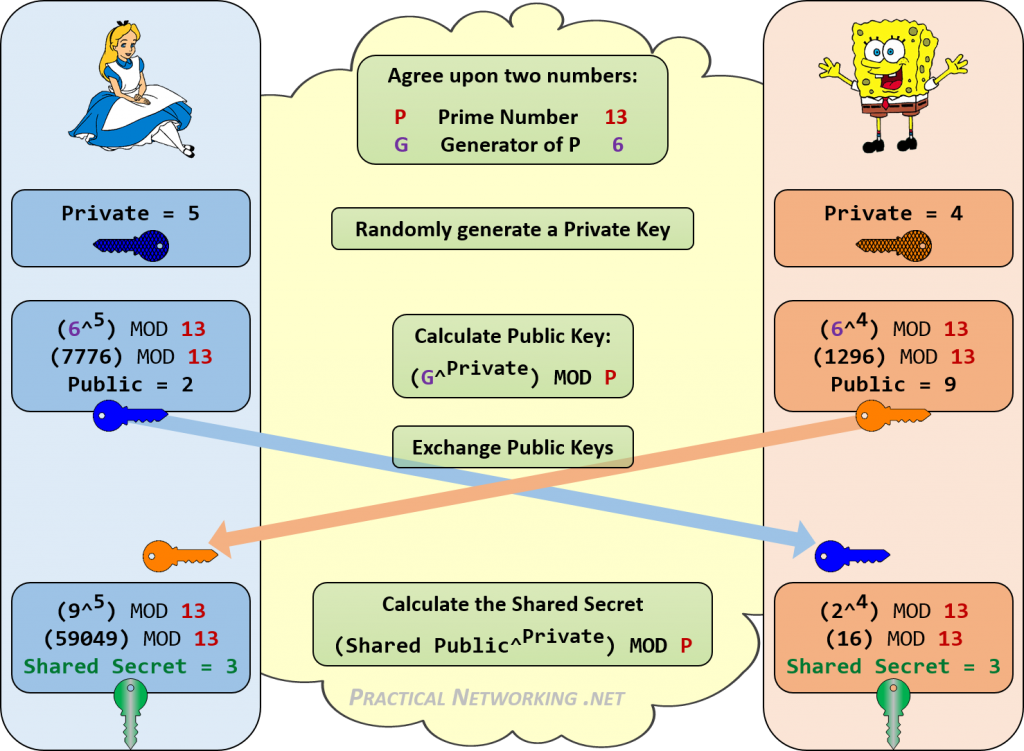
merk op hoe zowel Alice als Bob hetzelfde gedeelde geheim van 3 konden bereiken. Iedereen die meeluistert op zijn DH-sleuteluitwisseling zou alleen de publieke waarden kennen, en de beginwaarden P en G. Er is geen consistente manier om deze getallen (13, 6, 2, 9) te combineren om 3 te bereiken.

DH-getallen

in ons voorbeeld hebben we een priemgetal van 13 gebruikt. Aangezien dit priemgetal ook wordt gebruikt als de Modulus voor elke berekening, kan de volledige sleutelruimte voor het resulterende gedeelde geheim alleen maar 0-12 zijn. Hoe groter dit aantal, hoe moeilijker een tijd een aanvaller zal hebben in brute forceren van uw gedeelde geheim.

uiteraard gebruikten we zeer kleine getallen hierboven om de wiskunde relatief eenvoudig te houden. Echte DH-uitwisselingen doen wiskunde op getallen die veel groter zijn. Er zijn drie typische maten aan de nummers in Diffie-Hellman:

de bitgrootte is een verwijzing naar het priemgetal. Dit komt direct overeen met de volledige sleutelruimte van het resulterende gedeelde geheim. Om u een idee te geven van hoe groot deze sleutelruimte is:

om een 768 bit nummer volledig uit te schrijven, hebt u 232 decimale cijfers nodig.
om een 1024-bit-nummer volledig uit te schrijven, hebt u 309 decimale cijfers nodig.
om een 1536-bit-nummer volledig uit te schrijven, hebt u 463 decimale cijfers nodig.

gebruikmakend van het gedeelde geheim

zodra het gedeelde geheim is bereikt, wordt het meestal gebruikt in de berekening om een gezamenlijke symmetrische encryptiesleutel en/of een gezamenlijke HMAC – sleutel vast te stellen-ook bekend als sessiesleutels.

maar het is belangrijk erop te wijzen dat het gedeelde geheim zelf niet direct als geheime sleutel gebruikt dient te worden. Als dat zo was, kunt u er alleen van verzekerd zijn dat u tijdens het beveiligde gesprek nog steeds spreekt met dezelfde partij die aan de andere kant van de Diffie-Hellman uitwisseling was.

u hebt echter nog steeds geen bevestiging of zekerheid over wie de andere partij is. Alleen dat niemand anders plotseling kan doen alsof ze in het midden van uw beveiligde gesprek.

het genereren van de werkelijke sessiesleutels zou het gedeelde DH-geheim moeten bevatten, samen met een andere waarde die alleen bekend zou zijn bij de beoogde andere partij, zoals iets uit het Authenticatieschema dat u hebt gekozen.

video-inhoud verkiezen boven tekst? Het grootste deel van dit artikel is opgenomen en kan worden bekeken op Youtube:

Reeksnavigatie RSA voorbeeld >>