vilka ACT Math Formulas ska eleverna känna till och Tips för att memorera dem?
ACT Math avsnitt omfattar 60 fem – flervalsfrågor som eleverna ska svara på inom 60 minuter. Frågorna är hämtade från sex ämnesområden som omfattas upp till 11: e klass. De inkluderar Pre-algebra, mellanliggande algebra, elementär algebra, koordinatgeometri, trigonometri och plangeometri.
här är de ämnen och färdigheter som omfattas av Math ACT-testet.
Algebra
avsnittet innehåller 14 frågor och testar studenten på decimaler, heltal, bråk, förhållande, positiva heltal, heltal, kvadratrötter, procent och andel. Andra testade ämnen inkluderar en variabel, linjära ekvationer, absolutvärde, multiplar och faktorer, median, medelvärde, läge, datatolkning och räkneproblem och sannolikhet.
Intermediate Algebra
denna del består av nio frågor som testar studenten i ojämlikheter, absolutvärde, kvadratisk formel, ekvationssystem, rationella och radikala uttryck, funktioner, kvadratiska ojämlikheter, polynom, matriser och komplexa tal.
elementär Algebra
det kommer att finnas cirka tio frågor i området som berör polynom, variabler, factoring, heltal exponenter, kvadratrötter, linjära ojämlikheter och kvadratiska ekvationer.
Plangeometri
du kommer att ha 14 frågor som berör planfigurer som rektanglar, parallellogram, trianglar, trapezoider och cirklar. Vissa frågor testar kunskap om vinkelräta linjer, rotationer, 3D-geometri, Område, Omkrets, logiskt resonemang, volym, översättningar och reflektioner.
koordinatgeometri
det kommer cirka nio frågor från områdestestningen på grafen över punkter, tallinjediagram, cirklar, polynom, linjer, kurvor, mittpunktsformel, koner, transformationer, avståndsformel, ekvationer och grafförhållanden, lutning och egenskaper hos vinkelräta och parallella linjer.
i avsnittet hittar Trigonometri fyra frågor om trigonometriska funktioner, ekvationer och identiteter, rätt triangel trigonometriska förhållanden och trigonometriska funktioner modellering.
lista över ACT matematiska formler
här är en lista över 13 ACT matematiska formler du behöver veta för ACT-testet:
- aritmetiskt medelvärde
- Sannolikhet
- kvadratisk ekvation
- Distance Formula
- Slope Formula
- Slope Intercept Formula
- Midpoint Formula
- area av en triangel
- Pythagoras sats
- område av rektangel och omkrets
- volym av kuboid
- område av en cirkel
- trigonometriska formler
aritmetiskt medelvärde
Detta är samma som genomsnittet, och det är summan av alla objekt dividerat med antalet objekt. Om du till exempel beräknar medelvärdet av värden delade du summan med antalet värden
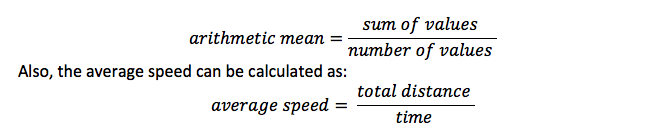
Sannolikhetsformel
Sannolikhet används vid beräkning av möjligheten att antalet gånger något kommer att inträffa i en uppsättning möjliga resultat. Det är en representation av chanserna att något händer. En sannolikhet på 1 betyder att det finns ett visst något som kommer att hända, men en möjlighet till 0 betyder att något inte kommer att hända.
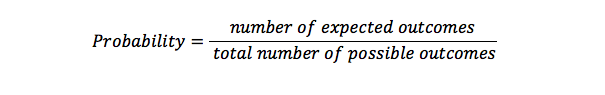
kvadratisk ekvation
formeln uttryckt som:
x = -B 2-4 AC/2a
används för att bestämma x-avlyssningarna av en parabolisk eller kvadratisk ekvation.
Distansformel
formeln används vid beräkning av avståndet mellan två punkter på ett koordinatplan. Formeln uttrycks som:
d = 2 + (x ^ – x₂) 2
Lutningsformel
lutningen är ett mått på linjeändringar uttryckta som y-axelförändringen dividera med förändringen på X-axeln (rise/run).
om du till exempel har punkt A (X1, Y1) och B( X2, Y2) kan du beräkna lutningen som:
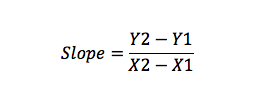
Lutningsavlyssningsformeln
lutningsavlyssningsformeln är en linjeekvation uttryckt som Y=MX + b i vilken:
- M står för linjens lutning, medan b är y-avlyssningen där y-avlyssningspunkten korsar y-axeln.
- om linjen kommer att passera genom ursprunget, är y-interceptet noll, och ekvationen kommer att uttryckas som Y=MX.
Mittpunktsformel
detta är en formel som hittar mittpunkten för en rad. Om du till exempel har två punkter, A (X1, Y1) och B( X2, Y2), kommer mittpunkten att vara:
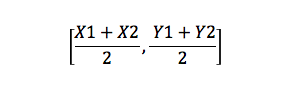
arean av en triangel
formeln uttryckt som XXL (bas x höjd) används för att beräkna den totala arean som är innesluten i en triangel.
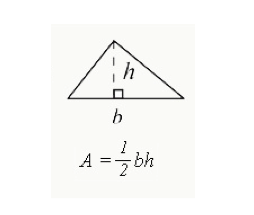
- b= basen av triangeln (kanten på ena sidan)
- h=höjden på en triangel. Höjden för en rätvinklig triangel kommer att vara sidan med en 90 graders vinkel. För andra trianglar kommer höjden att falla ner i triangeln, som visas ovan.
Pythagoras sats
Pythagoras sats är avgörande när man beräknar en rätvinklig triangels okända sida när två sidor är kända. Formeln uttrycks som a2 + b2=c2. Summan av två kortare sidor är lika med summan av den längre sidan.

område av rektangel och omkrets
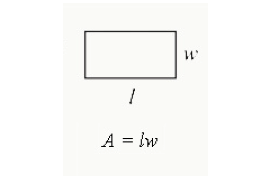
för att hitta en rektangels område multiplicerar du längden med bredden. Det är det totala området som är inneslutet i en rektangel.
Area = Längd x bredd
å andra sidan är en rektangels omkrets avståndet runt den.
Perimeter = (L+W+L+W) förenklad som 2 (L + W)
volym kuboid
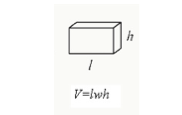
du kan beräkna en kuboids volym genom att multiplicera dess längd, bredd och höjd på kuboiden.
område av en cirkel
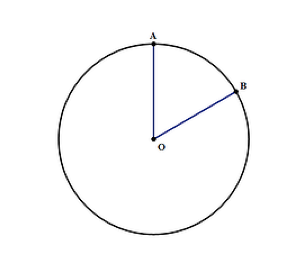
en cirkels område kan hittas med formeln nr2 där:
- det är en konstant som skrivs som 3.14, vilket är viktigt att komma ihåg om du inte kommer att ha en räknare under testet
- r-är cirkelns radie, som i diagrammet ovan. Det är avståndet från O till kanten av cirkeln vid punkt A eller B
på samma sätt kallas avståndet runt cirkeln som omkretsen. Det beräknas som:
cirkelns omkrets = nD eller 2nr
där:
- D, vilket är diametern är dubbelt cirkelns radie. Det är linjen som delar cirkeln i två halva rörande två ändar av en cirkel.
trigonometriska formler sinus (SOH), cosinus (CAH), Tangent (TOA)
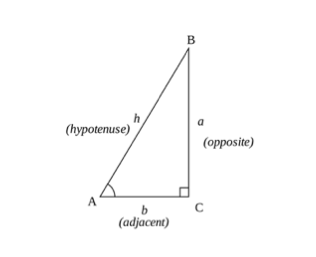
trigonometriska beräkningar kan summeras med grundläggande begrepp i en triangel med sinus -, cosinus-och tangentreglerna (SOHCAHTOA). Du kan beräkna cosinus, sinus eller tangent för en vinkel med hjälp av en triangels sidor.

där:
- motsatt sida-är triangelns sida som är motsatt vinkeln ()
- intilliggande sida – är den sida som är närmast vinkeln men inte den längsta sidan.
- hypotenusen är triangelns längsta sida.
Tips för att memorera ACT-matematiska formler och ekvationer
för att memorera formlerna under ACT-tentamen är det viktigt att bekanta dig tidigt genom att läsa i de ämnesområden som anges för matteprovet.
du kan också öva genom att försöka så många problem som möjligt för att behärska formeln.
att använda olika kanaler som att säga formlerna högre eller skriva dem på diagram och klistra in dem i ditt rum kan hjälpa dig att komma ihåg formlerna.