Diffie-Hellman

Hur kan två personer i ett trångt rum härleda en hemlighet som bara paret vet, utan att avslöja hemligheten för någon annan som kan lyssna?

det är exakt det scenario som Diffie-Hellman-Nyckelutbytet finns för att lösa.

Diffie-Hellman-Nyckelutbytet är ett sätt för två parter att gemensamt upprätta en delad hemlighet över en osäker kanal utan att ha någon förkunskap om varandra.

de utbyter aldrig hemligheten, bara några värden som båda kombinerar som låter dem uppnå samma resulterande värde.

konceptuellt är det bästa sättet att visualisera Diffie-Hellman-Nyckelutbytet med den allestädes närvarande färgblandningsdemonstrationen. Det är värt att snabbt granska det om du inte känner till det.

men i den här artikeln vill vi gå ett steg längre och faktiskt visa dig matematiken i Diffie-Hellman-Nyckelutbytet.

DH Math

innan du går in i matematiken i Diffie-Hellman, vill du ha en grundläggande förståelse för vad ett primtal är och vad Moduloperationen är (aka, Rest division). Båda dessa termer har definierats i en annan artikel.

nedan är en infographic som beskriver alla steg i Diffie-Hellman-utbytet mellan Alice och Bob.

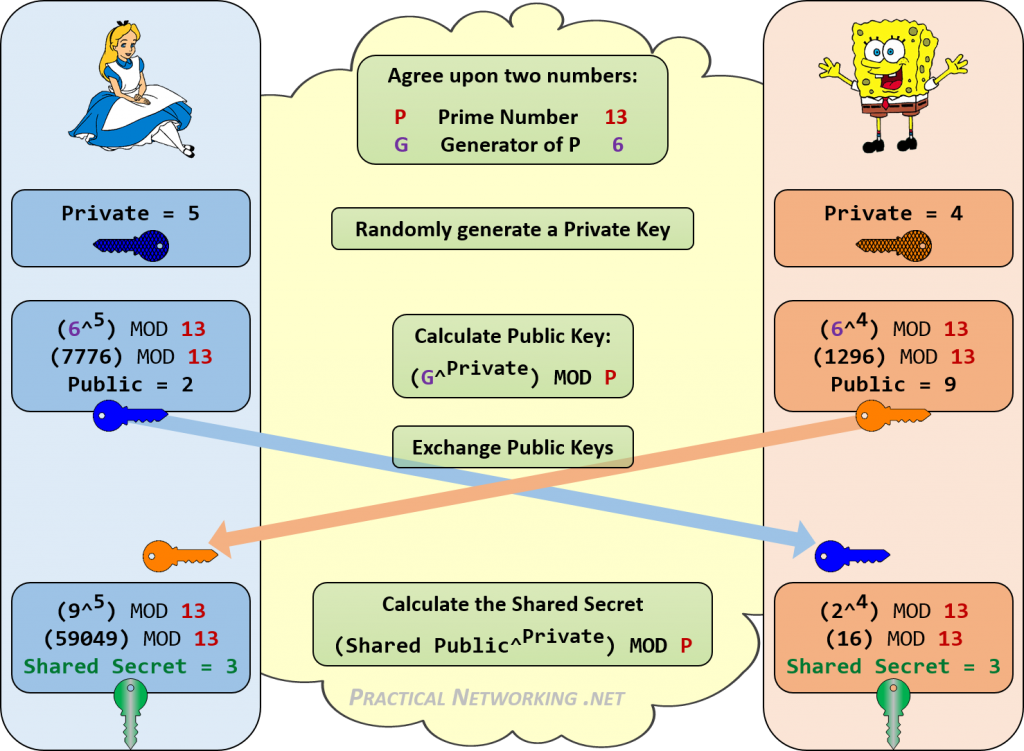
Lägg märke till hur både Alice och Bob kunde uppnå samma delade hemlighet av 3. Den som lyssnar på deras Dh-nyckelutbyte skulle bara känna till de offentliga värdena och start-p-och G-värdena. Det finns inget konsekvent sätt att kombinera dessa siffror (13, 6, 2, 9) för att uppnå 3.

Dh-nummer

i vårt exempel använde vi ett primtal på 13. Eftersom detta primtal också används som modul för varje beräkning kan hela nyckelutrymmet för den resulterande delade hemligheten bara vara 0-12. Ju större detta nummer, desto svårare en tid en angripare kommer att ha i brute tvinga din delade hemlighet.

självklart använde vi mycket små siffror ovan för att hålla matematiken relativt enkel. Sanna dh-utbyten gör matte på siffror som är mycket större. Det finns tre typiska storlekar på siffrorna i Diffie-Hellman:

bitstorleken är en referens till primtalet. Detta motsvarar direkt hela nyckelutrymmet för den resulterande delade hemligheten. För att ge dig en uppfattning om hur stor denna nyckel utrymme är:

för att fullt ut skriva ut en 768 bitars nummer, skulle du behöva 232 decimaler.
för att fullt ut skriva ut ett 1024 bitars nummer behöver du 309 decimaler.
för att fullt ut skriva ut ett 1536 bitnummer behöver du 463 decimaler.

använda den delade hemligheten

när den delade hemligheten har uppnåtts används den vanligtvis i beräkningen för att upprätta en gemensam symmetrisk krypteringsnyckel och/eller en gemensam HMAC – Nyckel-även känd som sessionsnycklar.

men det är viktigt att påpeka att den delade hemligheten inte direkt ska användas som den hemliga nyckeln. Om det var, allt du kan vara säker på är att under hela den säkra konversationen talar du fortfarande med samma parti som var på andra sidan Diffie-Hellman-utbytet.

du har dock fortfarande ingen bekräftelse eller försäkran om vem den andra parten är. Bara att ingen annan plötsligt kan låtsas vara dem mitt i din säkra konversation.

genereringen av de faktiska Sessionsnycklarna bör innehålla Dh-delad hemlighet, tillsammans med något annat värde som bara skulle vara känt för den avsedda andra parten, som något från det autentiseringsschema du valde.

föredrar du videoinnehåll framför text? Majoriteten av denna artikel har spelats in och kan ses på Youtube:

serie navigering RSA exempel >>