ACT Math Formulat

What ACT Math Formulat Should Student Know and Tips To Memorize Them?

ACT Math-osio sisältää 60 viiden monivalintakysymystä, joihin opiskelijan tulee vastata 60 minuutin kuluessa. Kysymykset arvotaan kuudesta aihealueesta, joita käsitellään 11. luokkaan asti. Niitä ovat Esialgebra, välialgebra, alkeisalgebra, koordinaattigeometria, Trigonometria ja tasogeometria.

tässä ovat Matematiikkalakikokeessa käsitellyt aiheet ja taidot.

Algebra

jakso käsittää 14 kysymystä ja testiä oppilaalle desimaaleista, kokonaisluvuista, murtoluvuista, suhdeluvuista, positiivisista kokonaislukuvoimista, kokonaisluvuista, neliöjuurista, prosenteista ja osuudesta. Muita testattuja aiheita ovat yksi muuttuja, lineaariset yhtälöt, itseisarvo, kerrannaiset ja tekijät, mediaani, keskiarvo, tila, tietojen tulkinta sekä laskuongelmat ja todennäköisyys.

väli-Algebra

tämä osa käsittää yhdeksän kysymystä, jotka testaavat opiskelijaa epätasa-arvoissa, itseisarvossa, neliökaavassa, yhtälön, rationaalisten ja radikaalien lausekkeiden, funktioiden, quadraticin epäyhtälöissä, polynomeissa, matriiseissa ja kompleksiluvuissa.

alkeet Algebra

siellä on noin kymmenen kysymystä alalla koskevat polynomi, muuttujat, factoring, kokonaisluku eksponentit, neliöjuuret, lineaarinen eriarvoisuutta, ja quadratic yhtälöt.

Tasogeometria

sinulla on 14 kysymystä, jotka koskevat tasolukuja, kuten suorakulmioita, parallelogrammeja, kolmioita, puolisuunnikkaita ja ympyröitä. Joissakin kysymyksissä testataan tietoa kohtisuorista linjoista, rotaatioista, 3-D-geometriasta, alueesta, ympärysmitasta, loogisesta päättelystä, tilavuudesta, käännöksistä ja heijastuksista.

Koordinaattigeometria

alueella testataan noin yhdeksän kysymystä pisteiden kuvaajasta, lukujonokaavioista, ympyröistä, polynomeista, linjoista, käyristä, midpoint-kaavasta, coniceista, muunnoksista, etäisyyskaavasta, yhtälöistä ja kuvaajasuhteista, kaltevuudesta ja kohtisuorien ja yhdensuuntaisten viivojen ominaisuuksista.

jaksossa Trigonometria löytää neljä kysymystä trigonometrisistä funktioista, yhtälöistä ja identiteeteistä, suorakulmaisen kolmion trigonometrisistä suhdeluvuista ja trigonometristen funktioiden mallintamisesta.

luettelo NÄYTÖSMATEMATIIKAN kaavoista

tässä on luettelo 13 NÄYTÖSMATEMATIIKAN kaavoista, jotka sinun tulee tietää NÄYTÖSKOETTA varten:

1. aritmeettinen keskiarvo
2. todennäköisyys
3. Neliöyhtälö
4. Etäisyys Formula_9936>
5. kulmakerroin Formula_9936>
6. keskipiste Formula_9936>
7. kolmion pinta-ala
8. Pythagoraan lause
9. suorakulmion ja ympärysmitan pinta-ala
10. Kuutiollisen tilavuus
11. ympyrän pinta-ala
12. trigonometriset kaavat

aritmeettinen keskiarvo

tämä on sama kuin keskiarvo, ja se on summa kaikista eristä jaettuna erien lukumäärällä. Esimerkiksi arvojen keskiarvoa laskettaessa jaetaan summa arvojen lukumäärällä

act-exam-aritmeettinen keskiarvo-formula_8874>

todennäköisyys Formula_8071 >

todennäköisyydellä. Se kuvaa mahdollisuuksia, että jotain tapahtuu. Todennäköisyys 1 tarkoittaa, että on olemassa tietty jotain, joka tapahtuu, mutta mahdollisuus 0 tarkoittaa, että jotain ei tapahdu.

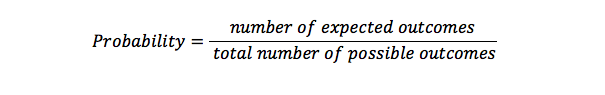
Neliöyhtälö

kaava ilmaistuna:

x = – b ± √b2-4ac/2a

sitä käytetään parabolisen tai kvadraattisen yhtälön x-interceptien määrittämiseen.

Etäisyys Formula_8071>

kaavaa käytetään laskettaessa kahden pisteen välistä etäisyyttä koordinaattitasolla. Laskukaava ilmaistaan seuraavasti:

d = √(x₁ – xβ)2 + (y₁ – yβ)2

kulmakerroin Formula_8071>

kulmakerroin on janan muutosten mitta, joka ilmaistaan Y-akselin muutoksena jaettuna X-akselin muutoksella (nousu/juoksu).

esimerkiksi, jos sinulla on piste A (X1, Y1) ja B (X2, Y2), voit laskea kulmakertymän seuraavasti:

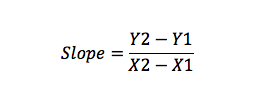
kulmakertoimen Formula_8071>

kulmakertoimen kaava on viivayhtälö, joka ilmaistaan muodossa Y=MX+b, jossa:

• M tarkoittaa linjan kaltevuutta, kun taas b on y-leikkauspiste, jossa y-leikkauspiste ylittää y-akselin.
• jos suora kulkee Origon kautta, niin y-leikkaus on nolla, ja yhtälö ilmaistaan muodossa Y=MX.

keskipiste Formula_8071>

tämä on kaava, joka löytää suoran keskipisteen. Jos on esimerkiksi kaksi pistettä, A(X1, Y1) ja B(X2, Y2), niin keskipiste on:

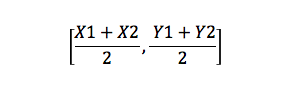
kolmion pinta-ala

kolmion sisään suljetun kokonaispinta-alan laskemiseksi käytetään½: na ilmaistua kaavaa (perus-x Korkeus).

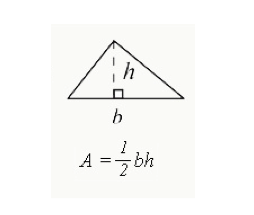
• b=kolmion pohja (yhden sivun reuna)
• h = kolmion korkeus. Suorakulmaisen kolmion korkeus on sivu, jonka kulma on 90 astetta. Muiden kolmiot, korkeus laskee alas sisätilojen kolmion, kuten edellä.

Pythagoraan lause

Pythagoraan lause on ratkaiseva laskettaessa oikeakulmaisen kolmion tuntematonta puolta, kun kaksi puolta tunnetaan. Formula_2+b2=c2. Kahden lyhyemmän sivun summa on yhtä suuri kuin pidemmän sivun summa.

suorakulmion ja kehän pinta-ala

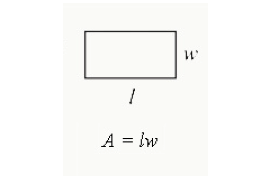
suorakulmion pinta-alan löytämiseksi kerrotaan pituus leveydellä. Se on suorakulmion sisään rajattu kokonaispinta-ala.

pinta-ala = pituus x Leveys

toisaalta suorakulmion kehä on sitä ympäröivä etäisyys.

Kehä = (L+W+L+W) yksinkertaistettuna 2 (L + W)

kuutiollinen tilavuus

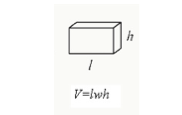
kuutiollisen tilavuuden voi laskea kertomalla sen pituuden, leveyden ja korkeuden kuutiosta.

ympyrän pinta-ala

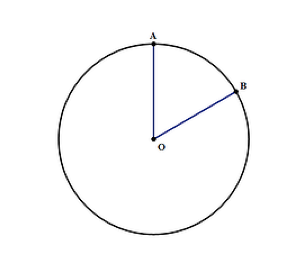
ympyrän pinta-ala voidaan löytää kaavalla formula_2, jossa:

• π on vakio, joka kirjoitetaan 3.14, joka on tärkeää muistaa, jos sinulla ei ole laskinta testin aikana
• r – on ympyrän säde, kuten yllä olevassa kaaviossa. Se on etäisyys O: sta ympyrän reunaan pisteessä A tai B

vastaavasti etäisyyttä ympyrän ympäri kutsutaan kehäksi. Se lasketaan seuraavasti:

ympyrän kehä = nD tai 2NR

missä:

• D, joka on halkaisija on kaksi kertaa ympyrän säde. Se on Jana, joka jakaa ympyrän kahteen puoleen, jotka koskettavat ympyrän kahta päätä.

trigonometriset kaavat Sini (SOH), kosini (CAH), tangentti (TOA)

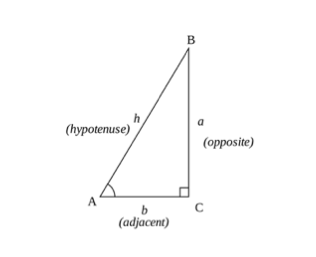
trigonometriset laskelmat voidaan summata kolmion peruskäsitteillä sini -, kosini-ja tangenttisääntöjen (SOHCAHTOA) avulla. Kulman kosinin, sinin tai tangentin voi laskea kolmion sivujen avulla.

jossa:

• vastakkainen sivu – on kolmion sivu, joka on vastakkainen kulman () kanssa
• viereinen sivu-on sivu, joka on lähimpänä kulmaa, mutta ei pisin sivu.
• hypotenuusa on kolmion pisin sivu.

vinkkejä LAKIMATEMATIIKAN kaavojen ja yhtälöiden muistamiseen

kaavojen ulkoa opettelemiseksi lakitutkinnon aikana on tärkeää perehtyä ajoissa lukemalla matematiikan kokeelle määriteltyjä aihealueita.

voit myös harjoitella yrittämällä mahdollisimman monia ongelmia kaavan hallitsemiseksi.

eri kanavien käyttäminen, kuten kaavojen sanominen kovempaa tai niiden kirjoittaminen kaavioihin ja niiden työntäminen omaan huoneeseen, voi auttaa muistamaan kaavoja.