Diffie-Hellman

miten kaksi täpötäydessä huoneessa olevaa ihmistä voi saada selville salaisuuden, jonka vain pari tietää, paljastamatta salaisuutta kenellekään muulle, joka saattaisi kuunnella?

juuri sitä skenaariota Diffie-Hellman-Avaimenvaihto on olemassa ratkaisemaan.

Diffie-Hellman-avainten vaihto on keino, jolla kaksi osapuolta voivat yhdessä luoda yhteisen salaisuuden salaamattomalle kanavalle ilman, että heillä on mitään ennakkotietoa toisistaan.

ne eivät koskaan varsinaisesti vaihda salaisuutta, vain joitakin arvoja, joita molempia yhdistää, minkä ansiosta ne saavuttavat saman tuloksena olevan arvon.

käsitteellisesti paras tapa visualisoida Diffie-Hellman-Avaimenvaihto on kaikkialla läsnä oleva maalivärien sekoittumisdemonstraatio. Se kannattaa tarkistaa nopeasti, jos et tunne sitä.

tässä artikkelissa haluamme kuitenkin mennä askeleen pidemmälle ja näyttää itse asiassa Diffie-Hellman-Avaimenvaihdon matematiikkaa.

DH-matematiikka

ennen Diffie-Hellmanin matematiikkaan siirtymistä halutaan saada perusymmärrys siitä, mikä on alkuluku ja mikä on Modulusoperaatio (eli loppujakauma). Molemmat termit on määritelty toisessa artikkelissa.

alla on infografiikka, jossa hahmotellaan kaikki Diffie-Hellman-vaihdon vaiheet Alicen ja Bobin välillä.

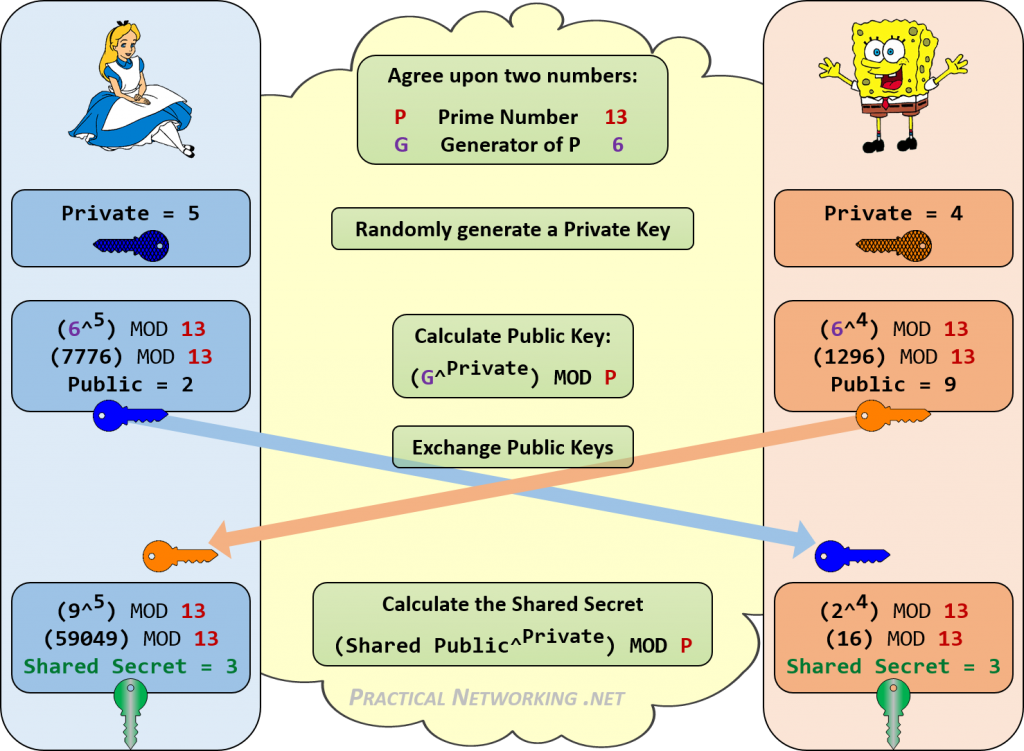
huomaa, kuinka sekä Alice että Bob onnistuivat saavuttamaan saman jaetun salaisuuden 3. Kuka tahansa kuuntelisi heidän DH-avaimensa vaihtoa, tietäisi vain julkiset arvot ja lähtöarvot P ja G. Ei ole olemassa johdonmukaista tapaa yhdistää näitä lukuja (13, 6, 2, 9) 3: n saavuttamiseksi.

DH-luvut

esimerkissämme käytimme alkulukua 13. Koska tätä alkulukua käytetään myös jokaisen laskennan Moduluksena, tuloksena olevan jaetun salaisuuden koko avainavaruus voi olla vain 0-12. Mitä suurempi luku, sitä vaikeampaa hyökkääjällä on – pakottaa yhteinen salaisuutenne.

ilmeisesti käytimme hyvin pieniä lukuja edellä auttaaksemme pitämään matematiikan suhteellisen yksinkertaisena. True DH pörssit tekevät matematiikkaa numerot, jotka ovat paljon suurempia. Diffie-Hellmanin numeroille on kolme tyypillistä kokoa:

bittikoko on viittaus Alkulukuun. Tämä vastaa suoraan tuloksena olevan jaetun salaisuuden koko avainavaruutta. Jotta saisit käsityksen siitä, kuinka suuri tämä avainavaruus on:

768-bittisen luvun kirjoittamiseen, tarvitset 232 desimaalilukua.
1024-bittisen luvun kirjoittamiseen tarvittaisiin 309 desimaalilukua.
1536-bittisen luvun kirjoittamiseen tarvittaisiin 463 desimaalilukua.

käyttämällä jaettua salaisuutta

kun jaettu salaisuus on saavutettu, sitä käytetään tyypillisesti laskennassa yhteisen symmetrisen salausavaimen ja/tai yhteisen HMAC – avaimen muodostamiseen-joka tunnetaan myös Istuntoavaimina.

on kuitenkin tärkeää huomauttaa, että itse jaettua salaisuutta ei tulisi suoraan käyttää salaisena avaimena. Jos olisi, voit olla varma vain siitä, että koko turvallisen keskustelun ajan puhut edelleen saman tahon kanssa, joka oli Diffie-Hellman-pörssin toisella puolella.

vielä ei kuitenkaan ole vahvistusta tai varmuutta siitä, kuka toinen osapuoli on. Vain, että kukaan muu ei voi yhtäkkiä teeskennellä olevansa he kesken turvallisen keskustelunne.

varsinaisten Istuntoavainten generoinnin tulisi sisältää jaettu DH-salaisuus sekä jokin muu arvo, joka olisi vain aiotun toisen osapuolen tiedossa, kuten jokin valitsemastasi Todennusjärjestelmästä.

mieluummin videosisältö kuin teksti? Suurin osa tästä artikkelista on nauhoitettu ja katsottavissa YouTubessa:

sarja Suunnistus RSA esimerkki > >