lineaarisen ekspansiivisuuden, pinta-alan ekspansiivisuuden ja tilavuuden tai kuutiollisen ekspansiivisuuden osalta ovat kaikki parametrit, joita hallitaan lämpöenergialla. Kaikki kolme parametri on riippuvainen lämpötilan nousu, joka on ensisijaisesti Celsius yksikkö lämpötilan.
Lineaarinen ekspansiivisuus riippuu lisäksi alkuperäisestä pituudesta ja lopullisesta pituudesta, pinta-alan ekspansiivisuus riippuu lisäksi alkuperäisestä pinta-alasta ja lopullisesta pinta-alasta ja lopuksi kuutiollinen eli tilavuusekspansiivisuus riippuu alkuperäisestä tilavuudesta ja lopullisesta tilavuudesta.
lineaarisen ekspansiivisuuden laskukaava on (l2 – l1) / l1θ
l2 edustaa lopullista pituutta.
l1 edustaa alkuperäistä pituutta.
θ kuvaa lämpötilan nousua celsiusasteina.
pinta – alan ekspansiivisuuden laskukaava on (A2-A1) / A1θ
A2 edustaa lopullista pinta-alaa.
A1 edustaa alkuperäistä aluetta.
θ kuvaa lämpötilan nousua celsiusasteina.
tilavuuden tai kuutiollisen ekspansiivisuuden laskukaava on (V2-V1) / V1θ
V2 edustaa lopullista tilavuutta.
V1 edustaa alkuperäistä nidettä.
θ kuvaa lämpötilan nousua celsiusasteina.
ratkaistaanpa kolme esimerkkiä lineaarisesta ekspansiivisuudesta, pinta-alan ekspansiivisuudesta ja tilavuudesta eli kuutiollisesta ekspansiivisuudesta. Calculator Encyclopedia (Nickzom Calculator) pystyy ratkaisemaan nämä parametrit, jotka osoittavat kaavat ja vastaavat tarkasti.
ennen kaikkea Nickzom-laskimeen on päästävä millä tahansa näistä keinoista:
- Web– https://www.nickzom.org/calculator-plus
- Android (maksullinen) – https://play.google.com/store/apps/details?id=org.nickzom.nickzomcalculator
- omena (maksettu) – https://itunes.apple.com/us/app/nickzom-calculator/id1331162702?mt=8
sitten, Siirry Laskin kartta, klikkaa lämpöenergia alla fysiikan osa
Esimerkki 1:
Etsi lineaarinen ekspansiivisuus (α) metallille, jonka alkuperäinen pituus on 8 cm ja lopullinen pituus 12 cm sen jälkeen, kun lämpötila on noussut 20°C.
α = (l2-l1) / l1θ
missä:
l2 (lopullinen pituus) = 12 cm
L1 (alkuperäinen pituus) = 8 cm
θ (lämpötilan nousu) = 20°C
näin ollen
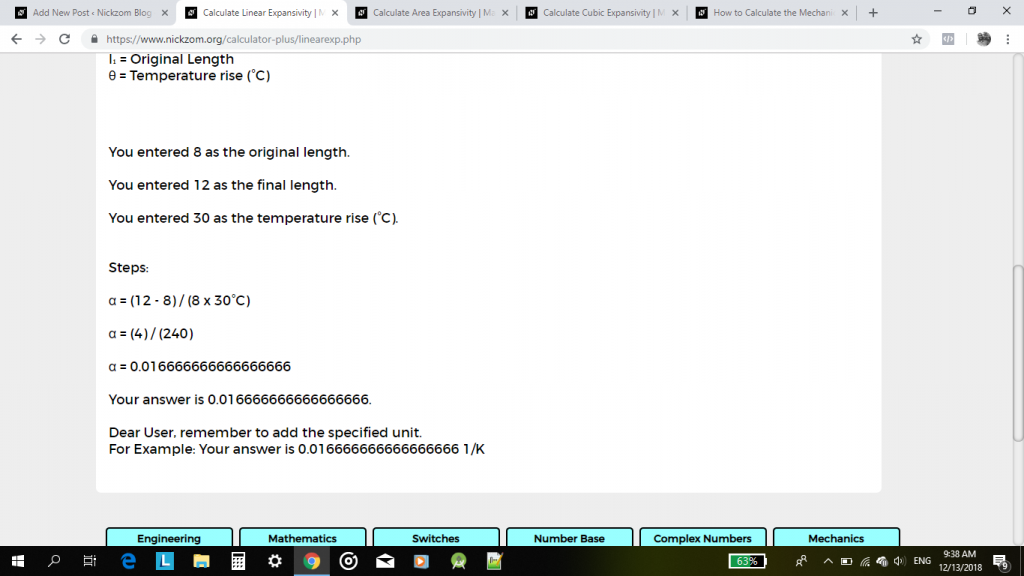
α = (12 – 8) / 8(20) 1/°
α = 4 / 160 1/°c
α = 0, 025 1 / °C
käyttämällä Nickzom-laskinta, klikkaa lineaarista laajuutta,
sitten, kirjoita arvot asianmukaisesti ja tarkasti
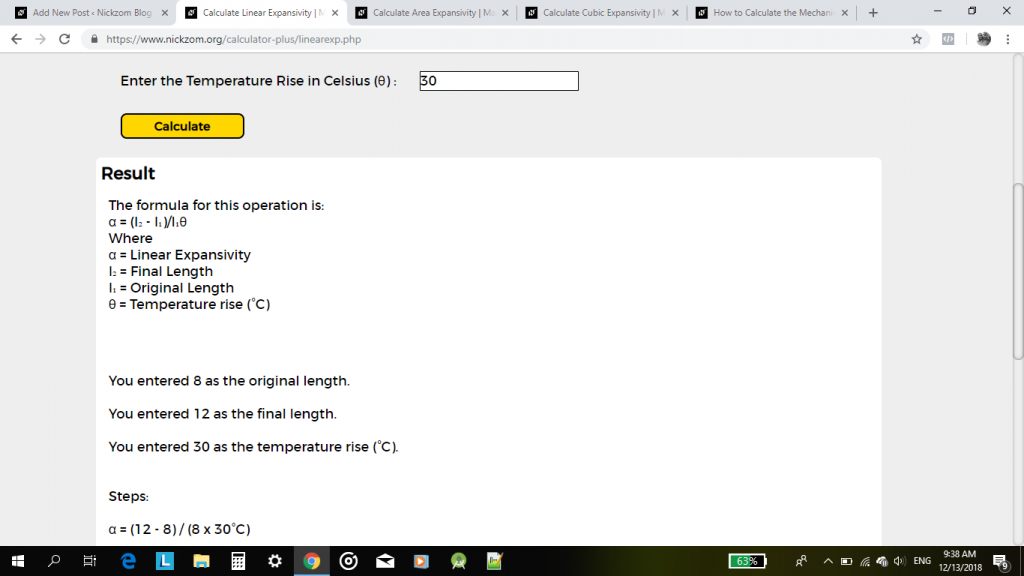
lopuksi, klikkaa Laske-painiketta
Esimerkki 2:
Etsi metallin pinta – ala, jossa sen alkuperäinen pinta-ala on 12 cm2 ja lopullinen pituus 20 cm2 sen jälkeen, kun lämpötila on noussut 30°C.
β = (A2-A1) / A1θ
missä:
A2 (lopullinen pinta-ala) = 20 cm2
A1 (Alkuperäinen ala) = 12 cm2
θ (lämpötilan nousu) = 30°C
siksi,
β = (20 – 12) / 12(30) 1/°C
β = 8 / 360 1/°c
β = 0.02222 1 / °C
käyttämällä Nickzom-laskinta, klikkaa alueen laajuutta,

sitten, kirjoita arvot asianmukaisesti ja tarkasti
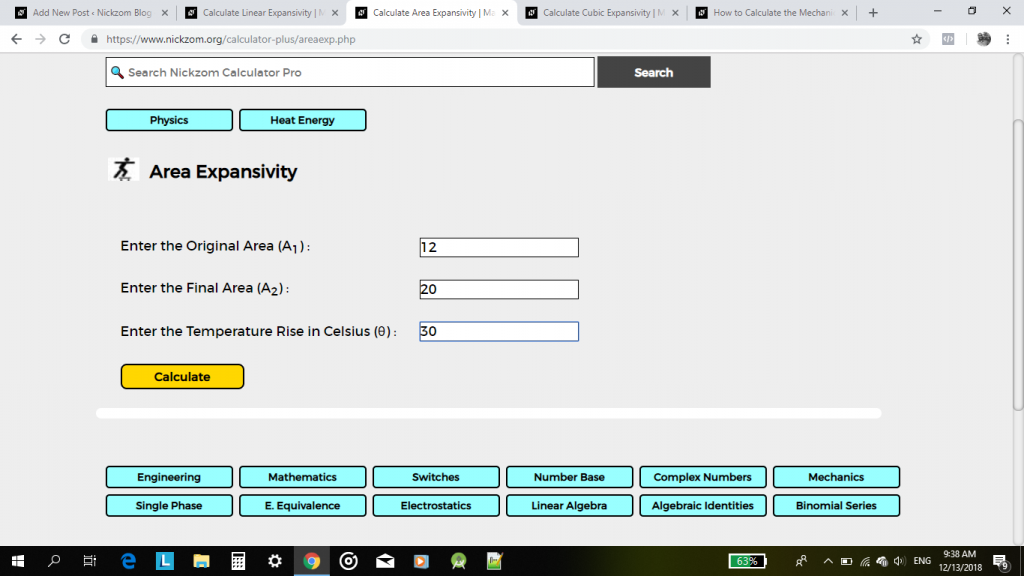
lopuksi, klikkaa Laske-painiketta

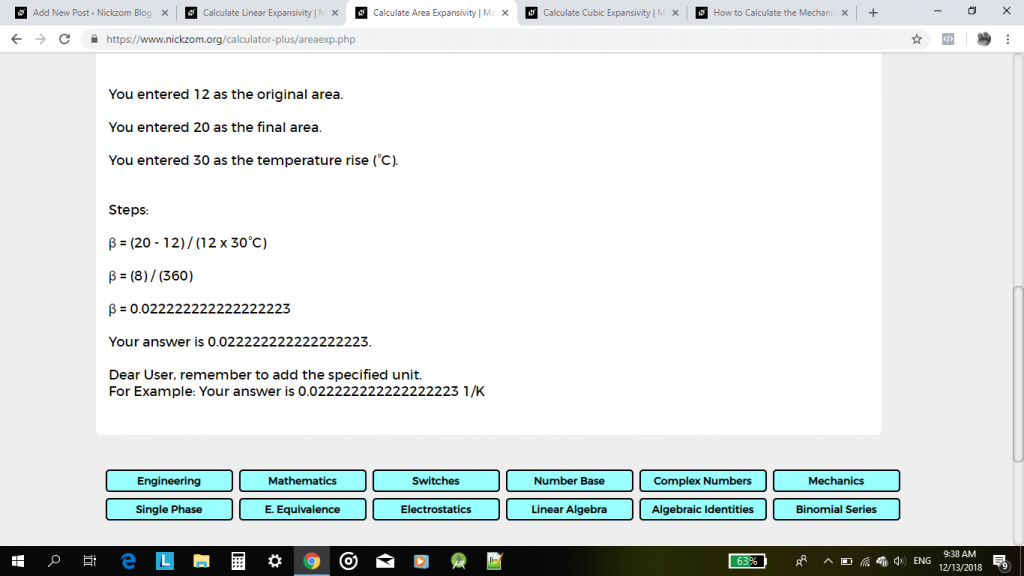
esimerkki 3:
Etsi metallin tilavuus tai kuutiollinen ekspansiivisuus (γ), kun sen alkuperäinen tilavuus on 18 cm3 ja lopullinen pituus 30 cm3 sen jälkeen, kun lämpötila on noussut 50°C.
γ = (V2-V1) / V1θ
missä:
V2 (lopullinen tilavuus) = 18 cm3
V1 (alkuperäinen tilavuus) = 30 cm3
θ (lämpötilan nousu) = 50°C
siksi