Risoluzione dei problemi facendo una lista

E ‘ stato utile? Condividilo con gli altri…

Facebook

Twitter

StumbleUpon

Come ho detto molte volte, uno dei principali obiettivi di educazione matematica è quello di suscitare fiducia per risolvere problemi. E mentre ci sono molti modi per risolvere i problemi di matematica, e noi come adulti possiamo spesso vedere le strategie come buon senso, queste sono cose che devono essere insegnate. Dare ai bambini il maggior numero possibile di strumenti li imposterà per il successo in modo da poter “lasciarli liberi” e vedere le loro menti creative lavorare ed esplorare. Per continuare la mia serie sull’insegnamento ai bambini di problem solve, oggi ho intenzione di discutere di problem solving facendo una lista.

Questo sembra così facile e diretto per un adulto, ma è davvero qualcosa che dovrebbe essere insegnato ai bambini in modo che abbiano gli strumenti di cui hanno bisogno per avere successo!

–>Pssst! I tuoi figli hanno bisogno di aiuto per dare un senso e risolvere i problemi di parole? Ti potrebbe piacere questo set di modelli di risoluzione dei problemi di word modificabili! Usali con qualsiasi livello di grado, per qualsiasi tipo di problema di parole:

Fare una lista significativa:

Questo è sempre stato un approccio difficile per me personalmente perché non sembra matematica e spesso può richiedere molto tempo. Voglio dire, chi vuole davvero sedersi e elencare tutte le possibili soluzioni a un problema di matematica? MA, si tratta di una strategia molto utile, e come vedremo, imparare ad essere organizzato e sistematico è la chiave (e sarà anche risparmiare tonnellate di tempo)!

Quindi quando è utile fare una lista? Fondamentalmente, ogni volta che hai un problema che ha più di una soluzione, o stai cercando di risolvere un problema di combinazione, è utile creare una lista.

Ma non solo un elenco di possibilità. Che si sentirà inutile e frustrante se si sta solo cercando di tirare fuori le possibilità da qualsiasi luogo. E più di questo, è molto probabile che le possibilità vengano saltate o ripetute, rendendo la soluzione finale sbagliata.

In cima a quello, sarà probabilmente più tempo per fare una lista se non si dispone di un approccio sistematico ad esso, che è probabilmente il motivo per cui non sono mai stato un fan come un bambino. Nessuno vuole solo sedersi e fissare la carta sperando soluzioni pop nel loro cervello.

Organizzare le informazioni in modo logico ti tiene in pista e assicura che tutte le possibili soluzioni saranno trovate.

Ci sono diversi modi per organizzare le informazioni, ma l’idea è di esaurire tutte le possibilità con una parte della tua lista prima di andare avanti.

Ad esempio, supponiamo che tu stia cercando di capire tutte le diverse combinazioni di condimenti per il gelato nella tua gelateria locale. Hanno 3 diversi gusti (cioccolato, vaniglia e fragola), ma hanno anche 4 diversi condimenti (noci, panna montata, caramelle al cioccolato e orsetti gommosi).

Se inizi a elencare diverse possibilità senza alcun tipo di struttura, sei destinato a perderti nella tua lista e perdere qualcosa. Quindi, invece, elencare tutte le possibilità per il gelato al cioccolato prima di passare alla vaniglia.

Cioccolato: solo cioccolato (senza condimenti), cioccolato con noci, cioccolato con panna montata, cioccolato con caramelle e cioccolato con orsetti gommosi.

Ora vediamo che ci sono 5 possibilità se si ottiene il gelato al cioccolato, e quindi possiamo passare alla vaniglia e poi alla fragola.

La chiave è iniziare con il primo sapore ed elencare ogni possibile topping in ordine. Quindi passare al sapore successivo e passare attraverso i condimenti nello stesso ordine.

Quindi nulla viene saltato, dimenticato o ripetuto. Dopo aver completato l’elenco, vediamo che ci sono 15 combinazioni possibili.

Alcuni studenti potrebbero anche notare che ci saranno 5 possibilità per ogni sapore, e quindi moltiplicare 3×5 senza completare l’elenco. (Questa è un’altra grande strategia: cercare i modelli).

Anche se un modello non viene scoperto, tuttavia, completando l’elenco in modo organizzato e sistematico assicurerà che tutte le possibilità siano coperte e il totale (15) trovato.

Un altro modo per organizzare l’elenco è creare un diagramma ad albero. Ecco un altro problema di esempio:

Sarah è in vacanza e ha portato 3 paia di pantaloni (blu, nero e bianco) e 3 camicie (rosa, giallo e verde). Quante diverse combinazioni vestito può fare?

l’Utilizzo di un diagramma ad albero è un ottimo modo per mantenere le informazioni organizzate, soprattutto se si hanno dei bambini che lottano con tenere traccia della loro lista:

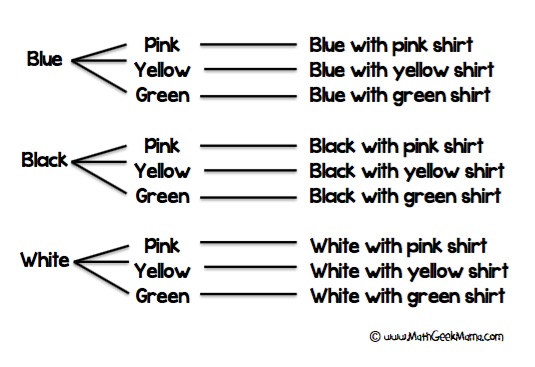
detta così sembra facile e semplice per un adulto, ma in realtà è qualcosa che dovrebbe essere insegnato ai bambini in modo da avere gli strumenti di cui hanno bisogno per avere successo!